CF1900C Anji's Binary Tree

Keksic 总是被 Anji 已读不回。通过一个共同的朋友，他发现 Anji 非常喜欢二叉树，于是决定帮她解决一个问题来吸引她的注意。 Anji 给了 Keksic 一棵有 $n$ 个结点的二叉树。结点 $1$ 是根节点，没有父节点。其他所有结点都有且仅有一个父节点。每个结点最多有 $2$ 个子节点，分别为左孩子和右孩子。对于每个结点，Anji 会告诉 Keksic 它的左孩子和右孩子的编号，或者告诉他不存在。 此外，每个结点上都写有一个字母 $s_i$，该字母为 'U'、'L' 或 'R'。 Keksic 的旅程从根节点开始，每一步他会执行以下操作： - 如果当前结点上的字母是 'U'，他会移动到它的父节点。如果父节点不存在，则什么也不做。 - 如果当前结点上的字母是 'L'，他会移动到它的左孩子。如果左孩子不存在，则什么也不做。 - 如果当前结点上的字母是 'R'，他会移动到它的右孩子。如果右孩子不存在，则什么也不做。 在旅程开始前，他可以进行如下操作：选择任意一个结点，将其上的字母替换为另一个字母。你需要求出他最少需要进行多少次这样的操作，使得在旅程开始后，他最终一定能够到达某个叶子结点。叶子结点指的是没有任何子节点的结点。到达哪个叶子结点无所谓。注意，他只需要能够到达叶子结点，不要求到达后停留在叶子结点，也不关心到达叶子结点前需要移动多少次。 请帮助 Keksic 改造 Anji 的树，让他能够赢得她的芳心，并让她来到 Čačak。

每个测试包含多个测试用例。第一行包含一个整数 $t$（$1 \le t \le 5 \cdot 10^4$）——表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$2 \le n \le 3 \cdot 10^5$）——树的结点数。 第二行包含一个长度为 $n$ 的字符串 $s$——每个结点上写的字母。保证 $s$ 只包含 'U'、'L' 和 'R'。 接下来的 $n$ 行，每行包含两个整数 $l_i$ 和 $r_i$（$0 \le l_i, r_i \le n$）——表示第 $i$ 个结点的左孩子和右孩子的编号。如果 $l_i = 0$，表示第 $i$ 个结点没有左孩子；如果 $r_i = 0$，表示第 $i$ 个结点没有右孩子。保证这些数据描述了一棵以 $1$ 为根的合法二叉树。 保证所有测试用例中 $n$ 的总和不超过 $3 \cdot 10^5$。

对于每个测试用例，输出一个整数——Keksic 需要进行的最少操作次数，使他能够到达某个叶子结点。

在第一个测试用例中，结点 $1$ 的左孩子是 $2$，右孩子是 $3$。结点 $2$ 和 $3$ 都没有子节点，因此是叶子结点。由于结点 $1$ 上写的是 'L'，Keksic 会移动到结点 $2$，因此不需要进行任何操作。 在第二个测试用例中，结点 $1$ 的左孩子是 $3$，右孩子是 $2$。结点 $2$ 和 $3$ 都是叶子结点。由于结点 $1$ 上写的是 'U'，Keksic 需要将其改为 'L' 或 'R'，才能到达叶子结点。 在第三个测试用例中，结点 $1$ 只有右孩子 $2$。由于结点 $1$ 上写的是 'L'，Keksic 需要将其改为 'R'，否则会被困在结点 $1$。 在第四个测试用例中，他可以修改 $3$ 个字符，使得各结点上的字母变为 "LURL"，这样他就能到达结点 $2$。 在第五个测试用例中，有 $3$ 个叶子结点，分别是 $3$、$6$ 和 $7$。要到达叶子结点 $6$ 或 $7$，他需要修改 $2$ 个字符。但如果将结点 $1$ 上的字母改为 'R'，他就能到达叶子结点 $3$，因此答案是 $1$。 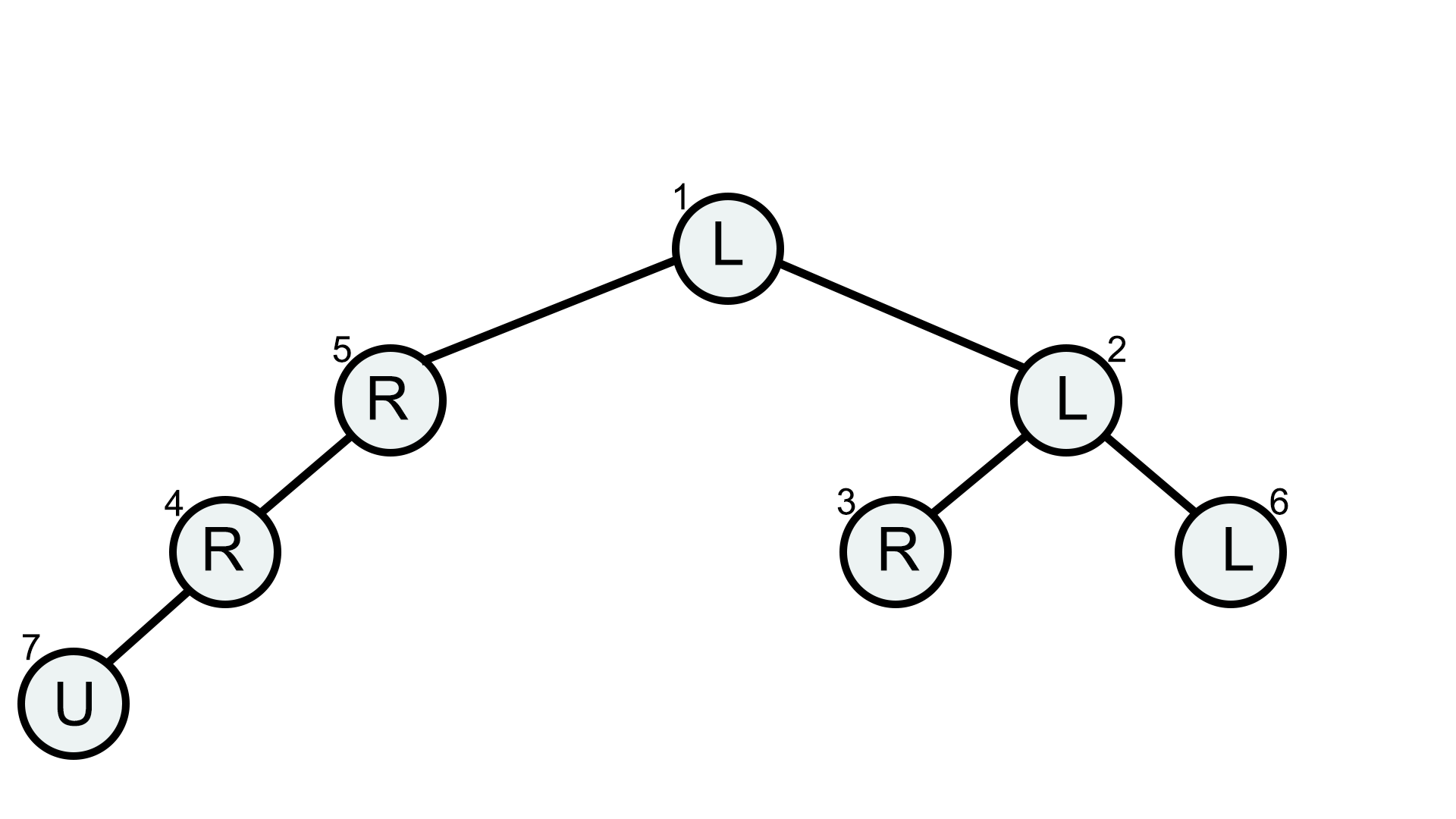 测试用例 5 的初始树。 由 ChatGPT 4.1 翻译