CF1903F Babysitting

Theofanis wants to play video games, however he should also take care of his sister. Since Theofanis is a CS major, he found a way to do both. He will install some cameras in his house in order to make sure his sister is okay. His house is an undirected graph with $ n $ nodes and $ m $ edges. His sister likes to play at the edges of the graph, so he has to install a camera to at least one endpoint of every edge of the graph. Theofanis wants to find a [vertex cover](https://en.wikipedia.org/wiki/Vertex_cover) that maximizes the minimum difference between indices of the chosen nodes. More formally, let $ a_1, a_2, \ldots, a_k $ be a vertex cover of the graph. Let the minimum difference between indices of the chosen nodes be the minimum $ \lvert a_i - a_j \rvert $ (where $ i \neq j $ ) out of the nodes that you chose. If $ k = 1 $ then we assume that the minimum difference between indices of the chosen nodes is $ n $ . Can you find the maximum possible minimum difference between indices of the chosen nodes over all vertex covers?

The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The first line of each test case contains two integers $ n $ and $ m $ ( $ 1 \le n \le 10^{5}, 1 \le m \le 2 \cdot 10^{5} $ ) — the number of nodes and the number of edges. The $ i $ -th of the following $ m $ lines in the test case contains two positive integers $ u_i $ and $ v_i $ ( $ 1 \le u_i,v_i \le n $ ), meaning that there exists an edge between them in the graph. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 10^{5} $ . It is guaranteed that the sum of $ m $ over all test cases does not exceed $ 2 \cdot 10^{5} $ .

For each test case, print the maximum minimum difference between indices of the chosen nodes over all vertex covers.

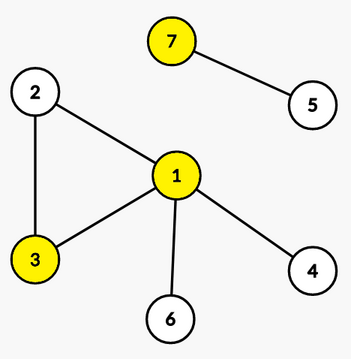In the first test case, we can install cameras at nodes $ 1 $ , $ 3 $ , and $ 7 $ , so the answer is $ 2 $ . In the second test case, we can install only one camera at node $ 1 $ , so the answer is $ 3 $ .