CF1905E One-X

In this sad world full of imperfections, ugly segment trees exist. A segment tree is a tree where each node represents a segment and has its number. A segment tree for an array of $ n $ elements can be built in a recursive manner. Let's say function $ \operatorname{build}(v,l,r) $ builds the segment tree rooted in the node with number $ v $ and it corresponds to the segment $ [l,r] $ . Now let's define $ \operatorname{build}(v,l,r) $ : - If $ l=r $ , this node $ v $ is a leaf so we stop adding more edges - Else, we add the edges $ (v, 2v) $ and $ (v, 2v+1) $ . Let $ m=\lfloor \frac{l+r}{2} \rfloor $ . Then we call $ \operatorname{build}(2v,l,m) $ and $ \operatorname{build}(2v+1,m+1,r) $ . So, the whole tree is built by calling $ \operatorname{build}(1,1,n) $ . Now Ibti will construct a segment tree for an array with $ n $ elements. He wants to find the sum of $ \operatorname{lca}^\dagger(S) $ , where $ S $ is a non-empty subset of leaves. Notice that there are exactly $ 2^n - 1 $ possible subsets. Since this sum can be very large, output it modulo $ 998\,244\,353 $ . $ ^\dagger\operatorname{lca}(S) $ is the number of the least common ancestor for the nodes that are in $ S $ .

Each test consists of multiple test cases. The first line contains a single integer $ t $ ( $ 1 \le t \le 10^3 $ ) — the number of test cases. The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 2 \le n \le 10^{18} $ ) — the length of the array for which the segment tree is built.

For each test case, output a single integer — the required sum modulo $ 998\,244\,353 $ .

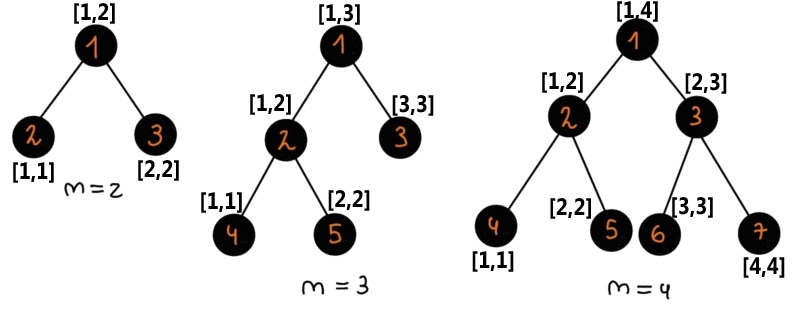In the first test case: Let's look at all subsets of leaves. - $ \operatorname{lca}(\{2\})=2 $ ; - $ \operatorname{lca}(\{3\})=3 $ ; - $ \operatorname{lca}(\{2,3\})=1 $ . Thus, the answer is $ 2+3+1=6 $ . In the second test case: Let's look at all subsets of leaves. - $ \operatorname{lca}(\{4\})=4 $ ; - $ \operatorname{lca}(\{5\})=5 $ ; - $ \operatorname{lca}(\{3\})=3 $ ; - $ \operatorname{lca}(\{4,5\})=2 $ ; - $ \operatorname{lca}(\{4,3\})=1 $ ; - $ \operatorname{lca}(\{5,3\})=1 $ ; - $ \operatorname{lca}(\{4,5,3\})=1 $ ; Thus, the answer is $ 4+5+3+2+1+1+1=17 $ .