CF1906I Contingency Plan 2

你在 ICPC 公司担任经理。在公司大楼里，有 $N$ 台计算机（编号从 $1$ 到 $N$）。有 $N-1$ 根网线，编号从 $1$ 到 $N-1$，这些网线将所有计算机连接成一个单一的网络。第 $i$ 根网线连接计算机 $U_i$ 和 $V_i$。每根网线都可以设置为应急模式，在这种模式下，第 $i$ 根网线只允许数据从 $U_i$ 传输到 $V_i$，而不能反向传输。在灾难发生时，所有网线都必须处于应急模式。 通过你的研究，你发现了一种新的方法来判断网络的脆弱性。你希望在当前网络的基础上添加零根或多根新网线，使得在灾难发生时网络不再脆弱。网络在且仅在存在唯一一个 $1$ 到 $N$ 的排列，使得对于所有连接计算机 $u$ 和 $v$ 的网线，$u$ 在排列中出现在 $v$ 之前时，网络才不脆弱。换句话说，网络应当恰好只有一个拓扑序。 下图展示了不脆弱网络和脆弱网络的示例。  对于不脆弱的网络，左侧和右侧网络唯一满足条件的排列分别为 $[1, 2, 3]$ 和 $[3, 1, 2]$。而对于脆弱的网络，左侧网络有 $2$ 个满足条件的排列：$[1, 2, 3]$ 和 $[3, 1, 2]$；右侧网络则没有任何满足条件的排列。 你想知道，最少需要添加多少根新网线，才能使当前网络在灾难发生时不再脆弱。此外，你还想知道，应该用最少数量的网线连接哪些计算机。如果有多种连接方式，你可以任选一种。在给定的约束下，可以证明一定存在一种方法使网络不再脆弱。

第一行包含一个整数 $N$（$2 \leq N \leq 100\,000$）。 接下来的 $N-1$ 行，每行包含两个整数 $U_i$ 和 $V_i$（$1 \leq U_i, V_i \leq N$）。输入的边构成一棵树。

第一行输出一个整数，表示为了使网络在灾难发生时不再脆弱，最少需要添加的新网线数量，记为 $K$，新网线编号从 $1$ 到 $K$。 如果 $K \neq 0$，则接下来输出 $K$ 行。每行包含两个整数 $A_i$ 和 $B_i$，表示第 $i$ 根新网线连接的两台计算机。在灾难发生时，第 $i$ 根新网线只允许数据从 $A_i$ 传输到 $B_i$，而不能反向传输。如果存在多种方案，你可以任选一种输出。

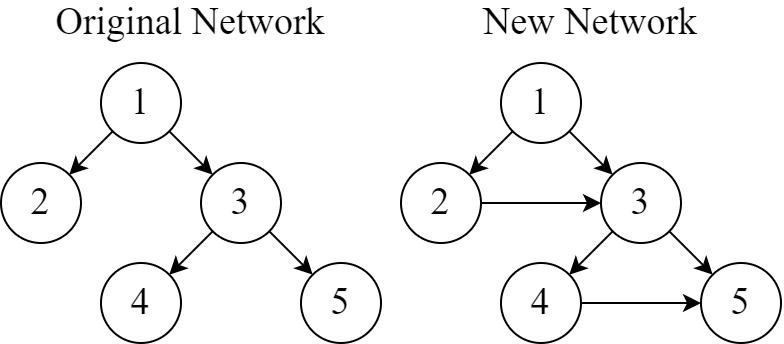
样例输入输出 #3 说明 下图展示了原始网络以及灾难发生时添加新网线后的新网络。唯一满足条件的排列为 $[1, 2, 3, 4, 5]$。  由 ChatGPT 4.1 翻译