CF1906M Triangle Construction

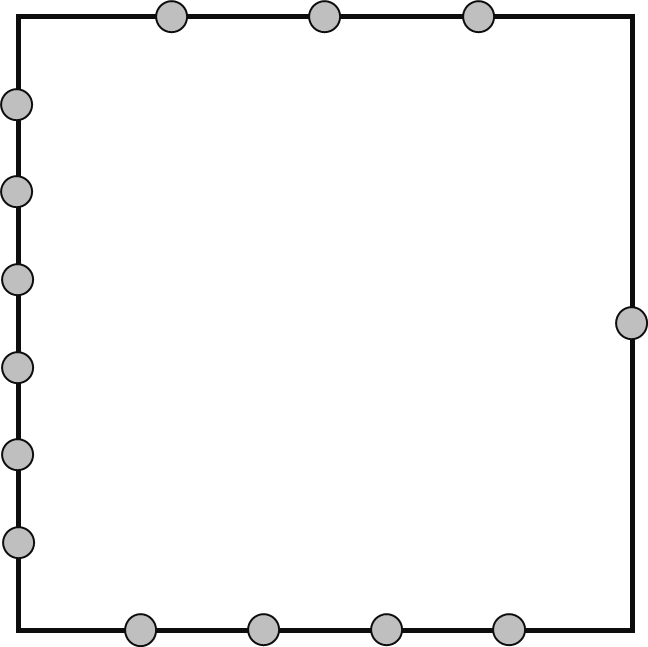
You are given a regular $ N $ -sided polygon. Label one arbitrary side as side $ 1 $ , then label the next sides in clockwise order as side $ 2 $ , $ 3 $ , $ \dots $ , $ N $ . There are $ A_i $ special points on side $ i $ . These points are positioned such that side $ i $ is divided into $ A_i + 1 $ segments with equal length. For instance, suppose that you have a regular $ 4 $ -sided polygon, i.e., a square. The following illustration shows how the special points are located within each side when $ A = [3, 1, 4, 6] $ . The uppermost side is labelled as side $ 1 $ . You want to create as many non-degenerate triangles as possible while satisfying the following requirements. Each triangle consists of $ 3 $ distinct special points (not necessarily from different sides) as its corners. Each special point can only become the corner of at most $ 1 $ triangle. All triangles must not intersect with each other. Determine the maximum number of non-degenerate triangles that you can create. A triangle is non-degenerate if it has a positive area.

The first line consists of an integer $ N $ ( $ 3 \leq N \leq 200\,000 $ ). The following line consists of $ N $ integers $ A_i $ ( $ 1 \leq A_i \leq 2 \cdot 10^9 $ ).

Output a single integer representing the maximum number of non-degenerate triangles that you can create.

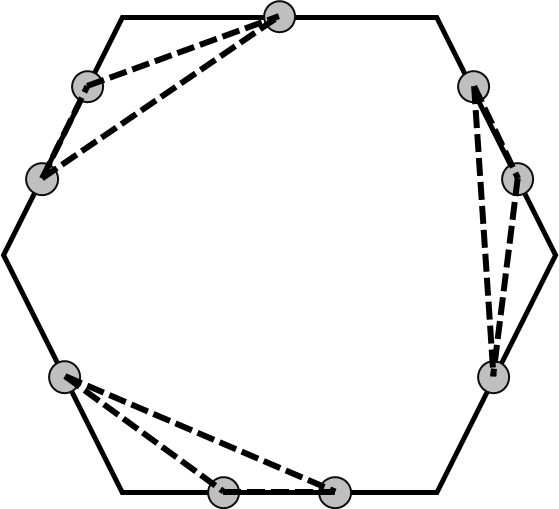
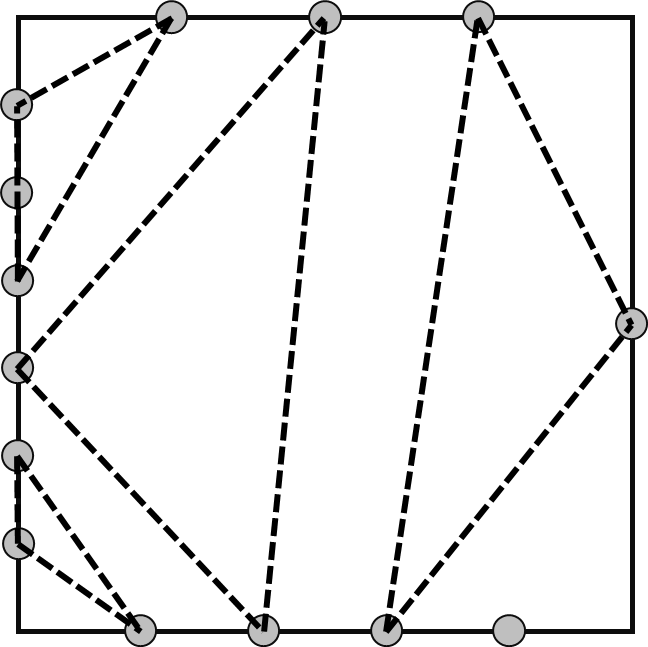
Explanation for the sample input/output #1 One possible construction which achieves maximum number of non-degenerate triangles can be seen in the following illustration. Explanation for the sample input/output #2 One possible construction which achieves maximum number of non-degenerate triangles can be seen in the following illustration.