CF1906M Triangle Construction

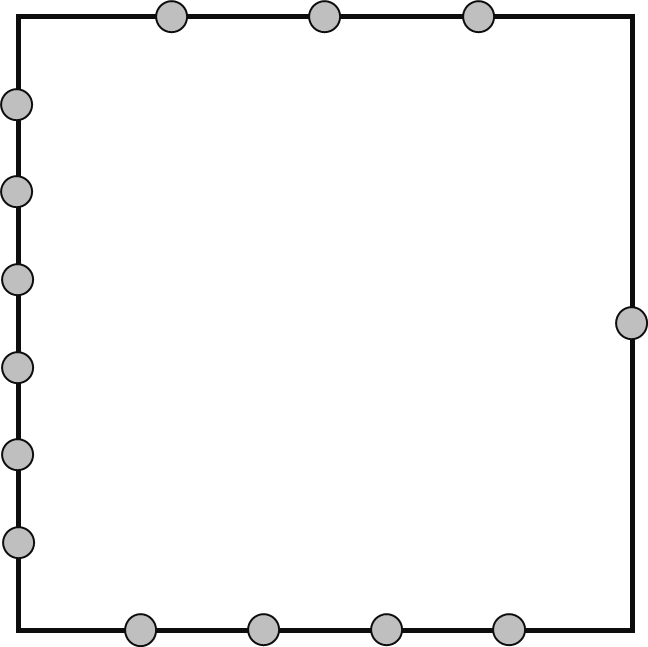
给定一个正 $N$ 边形。任选一条边标记为第 $1$ 条边，顺时针依次标记为第 $2$ 条边、第 $3$ 条边，直到第 $N$ 条边。第 $i$ 条边上有 $A_i$ 个特殊点，这些点的位置使得第 $i$ 条边被等分为 $A_i + 1$ 段。 例如，假设你有一个正四边形（即正方形）。下图展示了当 $A = [3, 1, 4, 6]$ 时，每条边上的特殊点的分布情况。最上方的边标记为第 $1$ 条边。  你希望在满足以下要求的前提下，构造尽可能多的不退化三角形。每个三角形由 $3$ 个不同的特殊点（不一定来自不同的边）作为顶点组成。每个特殊点最多只能作为 $1$ 个三角形的顶点。所有三角形之间不能相交。 请你求出最多可以构造多少个不退化三角形。 一个三角形是“不退化”的，当且仅当它的面积大于 $0$。

第一行包含一个整数 $N$（$3 \leq N \leq 200\,000$）。 第二行包含 $N$ 个整数 $A_i$（$1 \leq A_i \leq 2 \cdot 10^9$）。

输出一个整数，表示最多可以构造多少个不退化三角形。

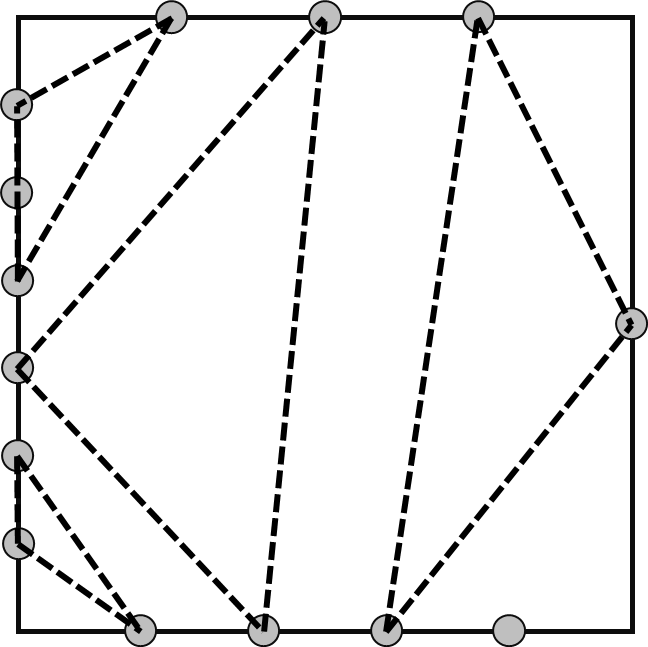
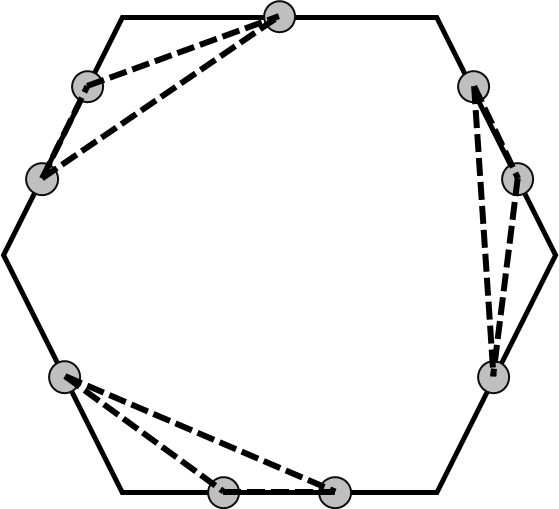
样例输入输出 $1$ 的解释： 下图展示了一种可以达到最大三角形数量的构造方式。  样例输入输出 $2$ 的解释： 下图展示了一种可以达到最大三角形数量的构造方式。  由 ChatGPT 4.1 翻译