CF1916E Happy Life in University

Egor 和他的朋友 Arseniy 今年即将高中毕业，很快就要进入大学了。由于他们非常有责任心，已经开始为入学做准备。 首先，他们决定先考虑未来四年学习期间的住宿问题。在浏览大学官网后，他们发现大学宿舍可以表示为一棵有 $n$ 个结点的有根树，根结点为 $1$。树中的每个结点代表一个带有某种活动类型 $a_i$ 的休闲区。两位朋友需要选择 $2$ 个休闲区（可以相同，也可以不同）作为他们的住宿地点。他们坚信，下面这个函数 $f(u, v) = diff(u, lca(u, v)) \cdot diff(v, lca(u, v))$ 的值越大，他们的生活就会越有趣。请帮助 Egor 和 Arseniy，找出所有休闲区对中 $f(u, v)$ 的最大值！ $^{\dagger} diff(u, v)$ —— 从结点 $u$ 到结点 $v$ 的简单路径上出现的不同活动类型的数量。 $^{\dagger} lca(u, v)$ —— 结点 $p$，它距离根结点最远，并且是 $u$ 和 $v$ 的祖先。

每组测试数据包含若干测试用例。第一行包含一个整数 $t$（$1 \le t \le 10^5$），表示测试用例的数量。接下来是每个测试用例的描述。 每个测试用例的第一行包含一个整数 $n$（$1 \le n \le 3 \cdot 10^{5}$）。 每个测试用例的第二行包含 $n-1$ 个整数 $p_2, p_3, \ldots, p_n$（$1 \le p_i \le i-1$），其中 $p_i$ 表示结点 $i$ 的父结点编号。 每个测试用例的第三行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$1 \le a_i \le n$），其中 $a_i$ 表示结点 $i$ 的活动编号。 保证所有测试用例中 $n$ 的总和不超过 $3 \cdot 10^5$。

对于每个测试用例，输出所有休闲区对 $(u, v)$ 中 $f(u, v)$ 的最大值。

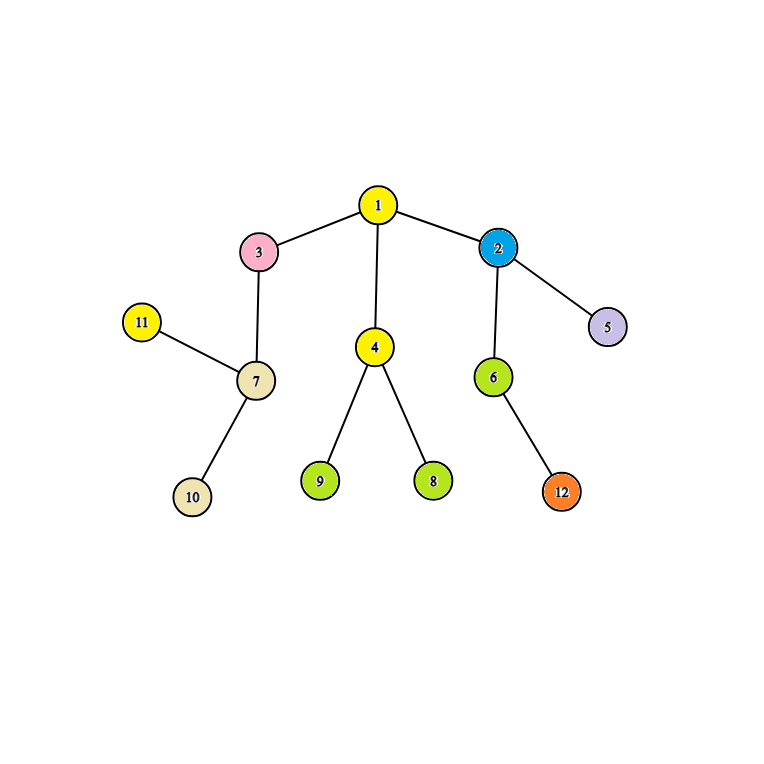
以第四个测试用例为例，树的结构如下：  所有休闲区都已着色。相同颜色表示休闲区的活动类型相同。考虑结点对 $(11, 12)$，$lca(11, 12) = 1$。从 $11$ 到 $1$ 的路径上的活动为 $[11, 5, 1, 11]$，其中有 $3$ 种不同的活动，因此 $diff(11, 1) = 3$。从 $12$ 到 $1$ 的路径上的活动为 $[7, 8, 2, 11]$，其中有 $4$ 种不同的活动，因此 $diff(12, 1) = 4$。因此 $f(11, 12) = diff(12, 1) \cdot diff(11, 1) = 4 \cdot 3 = 12$，这就是该树的答案。可以证明无法获得更优的答案。 由 ChatGPT 4.1 翻译