CF1916F Group Division
题目描述
在第 $31$ 中学,有两组奥林匹克竞赛选手:信息学组和数学组。信息学组有 $n_1$ 人,数学组有 $n_2$ 人。虽然具体每个人属于哪一组并不确定,但已知有些人之间存在友谊关系(这些关系可以是同组之间,也可以是不同组之间)。
这些关系非常牢固,即使移除任意一个人及其所有友谊关系后,任意两个人仍然可以直接或通过共同的朋友认识。
$^{\dagger}$ 更正式地说,若存在一组人 $a_1, a_2, \ldots, a_n$($1 \le a_i \le n_1 + n_2$),使得同时满足以下条件,则称两个人 $(x, y)$ 是相识的:
$\bullet$ $x$ 与 $a_1$ 直接相识。
$\bullet$ $a_n$ 与 $y$ 直接相识。
$\bullet$ 对于任意 $1 \le i \le n-1$,$a_i$ 与 $a_{i+1}$ 直接相识。
老师们对信息学选手和数学选手之间的友谊感到不满,因此他们决定将学生分成两组,使得满足以下两个条件:
$\bullet$ 信息学组有 $n_1$ 人,数学组有 $n_2$ 人。
$\bullet$ 任意一对信息学选手都应当相识(只允许通过同组的共同朋友间接相识),数学组选手也应如此。
请帮助他们解决这个问题,确定每个人属于哪一组。
输入格式
每个测试包含若干组数据。第一行包含一个整数 $t$($1 \le t \le 1000$),表示测试组数。接下来是每组测试数据的描述。
每组测试数据的第一行包含三个整数 $n_1$、$n_2$ 和 $m$($1 \le n_1, n_2 \le 2000$,$1 \le m \le 5000$)。$n_1$ 和 $n_2$ 分别为两组的人数,$m$ 为初始友谊关系数。
接下来的 $m$ 行,每行描述一对友谊关系:第 $i$ 行($1 \le i \le m$)包含两个整数 $(a, b)$,表示编号为 $a$ 和 $b$ 的两个人是朋友(关系是双向的)。
保证每组测试数据中所有友谊关系互不相同。
保证所有测试数据中 $n_1 + n_2$ 的总和不超过 $2000$,$m$ 的总和不超过 $5000$。
保证每组测试数据都存在解。
如果有多种分组方案,输出任意一种即可。
输出格式
对于每组测试数据,输出两行。
第一行输出 $n_1$ 个不同的整数 $a_i$($1 \le a_i \le n_1 + n_2$),表示属于第一组(信息学组)的人。
第二行输出 $n_2$ 个不同的整数 $b_i$($1 \le b_i \le n_1 + n_2$),表示属于第二组(数学组)的人。
所有编号必须互不相同。
如果有多种分组方案,输出任意一种。
说明/提示
以第三组测试数据为例,分组如下图所示:
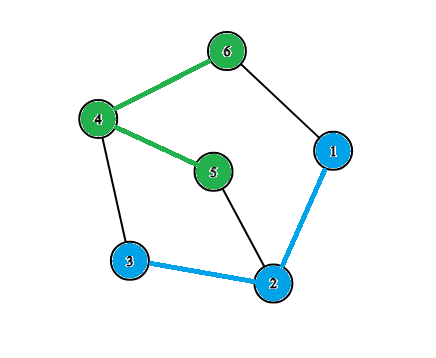
被选为信息学选手的学生用绿色表示,数学选手用蓝色表示。考虑所有信息学选手之间的相识关系:
$(4, 5), (4, 6)$ 是直接相识。
$(5, 6)$ 通过编号为 $4$ 的信息学选手间接相识。
再看所有数学选手之间的相识关系:
$(1, 2), (2, 3)$ 是直接相识。
$(1, 3)$ 通过编号为 $2$ 的数学选手间接相识。
可见,同组内任意两人都相识,因此该分组方案是正确的。
由 ChatGPT 4.1 翻译