CF1919D 01 Tree

有一棵带边权的完全二叉树，包含 $n$ 个叶子节点。完全二叉树的定义是：每个非叶子节点恰好有两个子节点。对于每个非叶子节点，我们将其两个子节点分别标记为左儿子和右儿子。 这棵二叉树有一个非常奇怪的性质：对于每个非叶子节点，指向其两个子节点的边中有一条权值为 $0$，另一条权值为 $1$。注意，权值为 $0$ 的边可以连接到左儿子或右儿子。 你已经忘记了这棵树的具体结构，但幸运的是，你还记得一些关于叶子的数组信息 $a$，数组大小为 $n$。对于每个 $i$（$1 \leq i \leq n$），$a_i$ 表示从根节点到第 $i$ 个叶子（按 dfs 顺序）的距离 $^\dagger$。请判断是否存在一棵满足数组 $a$ 的完全二叉树。你不需要重建这棵树。 $^\dagger$ 从顶点 $u$ 到顶点 $v$ 的距离定义为从 $u$ 到 $v$ 路径上所有边的权值之和。 $^\ddagger$ 叶子的 dfs 顺序通过对二叉树根节点调用如下 $\texttt{dfs}$ 函数获得。 ``` dfs_order = [] function dfs(v): if v is leaf: append v to the back of dfs_order else: dfs(left child of v) dfs(right child of v) dfs(root) ```

每组测试数据包含多组测试用例。第一行包含一个整数 $t$（$1 \leq t \leq 10^4$），表示测试用例的组数。接下来是每组测试用例的描述。 每组测试用例的第一行包含一个整数 $n$（$2 \le n \le 2\cdot 10^5$），表示数组 $a$ 的大小。 每组测试用例的第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$0 \le a_i \le n - 1$），表示从根到第 $i$ 个叶子的距离。 保证所有测试用例中 $n$ 的总和不超过 $2\cdot 10^5$。

对于每组测试用例，如果存在一棵满足数组 $a$ 的完全二叉树，输出 "YES"；否则输出 "NO"。 你可以以任意大小写输出每个字母（例如 "YES"、"Yes"、"yes"、"yEs" 都会被识别为肯定答案）。

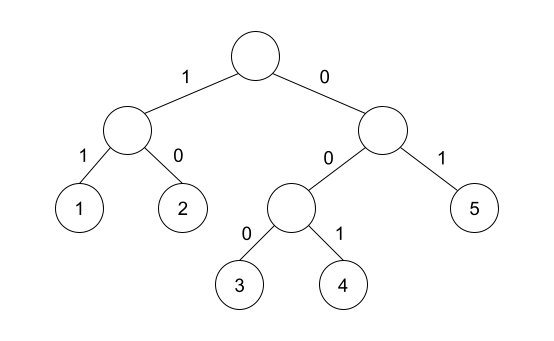
在第一个测试用例中，下图所示的树满足数组要求。  在第二个测试用例中，可以证明不存在满足数组要求的完全二叉树。 由 ChatGPT 4.1 翻译