CF191D Metro Scheme

贝尔兰非常重视隐私，因此几乎所有的规划和蓝图都是保密的。然而，邻国的一名间谍成功窃取了伯镇地铁的线路图。 伯镇地铁共有 $n$ 个车站，编号从 $1$ 到 $n$，有 $m$ 条双向隧道连接这些车站。整个伯镇地铁由线路组成。更准确地说，有两种类型的线路：环线和径向线。 一条径向线是一个车站序列 $v_{1},...,v_{k}$（$k > 1$），其中车站 $v_{i}$ 与 $v_{i+1}$（$i < k$）通过一条隧道相连，且每个车站在该线路中最多出现一次（对于 $i \neq j$，$v_{i} \neq v_{j}$）。 一条环线是一组车站 $v_{1},...,v_{k}$（$k > 2$），其中 $v_{i}$ 与 $v_{i+1}$ 通过一条隧道相连（对所有 $i < k$），并且 $v_{1}$ 与 $v_{k}$ 也通过一条隧道相连。同时，任意一个车站在该环线中最多只出现一次。 注意，一个车站可以被任意数量的线路经过。 按照贝尔兰的标准，不允许两站之间有多条隧道，且每条隧道恰好属于一条线路。当然，每条线路至少有一条隧道。任意两个车站之间都可以通过地铁隧道到达。从图论角度看，整张地铁图是一个顶点仙人掌图：如果我们把地铁看作一个图，车站是顶点，隧道是边，那么每个顶点至多属于一个简单环。 不幸的是，被间谍窃取的线路图只包含车站和隧道，无法判断每条隧道属于哪一条线路。为了成功破坏，间谍想要知道伯镇地铁可能的最少和最多线路数量。 请帮助他！

第一行包含两个整数 $n$ 和 $m$（$1 \leq n \leq 10^{5}$，$0 \leq m \leq 3 \cdot 10^{5}$），分别表示站点数量和隧道数量。 接下来的 $m$ 行中，每行包含两个整数，表示一条隧道连接的车站编号。车站编号为 $1$ 到 $n$ 的整数。 保证输入描述的图无重边和自环，图是连通的，且是顶点仙人掌图。

输出两个整数，分别表示最少和最多可能的线路数。

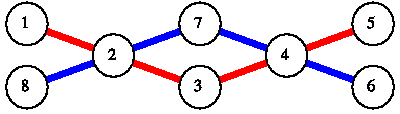
对于第二个样例，具有最少线路数量的地铁方案如下：  由 ChatGPT 5 翻译