CF1920F2 Smooth Sailing (Hard Version)

本题的两个版本唯一的区别在于 $q$ 的约束条件。只有当两个版本都被解决时，你才能进行 hack。 Thomas 正在环绕一个被海洋包围的岛屿航行。海洋和岛屿可以用一个有 $n$ 行 $m$ 列的网格表示。行从上到下编号为 $1$ 到 $n$，列从左到右编号为 $1$ 到 $m$。位于第 $r$ 行第 $c$ 列的格子可以表示为 $(r, c)$。下面是一个有效网格的示例。 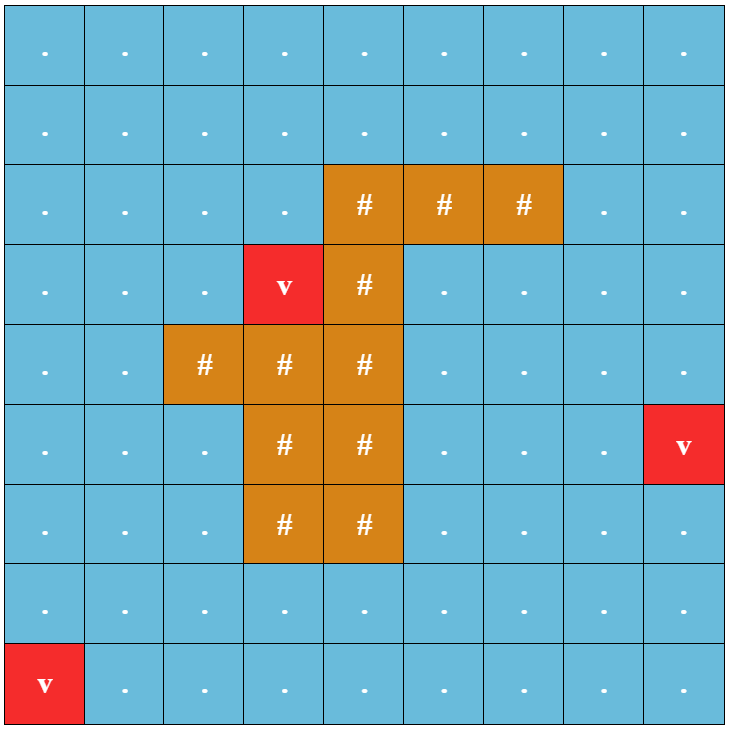 有效网格示例 网格中有三种类型的格子：岛屿、海洋和海底火山。用 '\#' 表示岛屿格子，'.' 表示海洋格子，'v' 表示海底火山格子。保证至少有一个岛屿格子和至少有一个海底火山格子。保证所有岛屿格子构成一个连通块 $^{\dagger}$，所有海洋格子和海底火山格子构成一个连通块。此外，保证网格的边界（即第 $1$ 行、第 $n$ 行、第 $1$ 列和第 $m$ 列）上没有岛屿格子。 定义从格子 $(x, y)$ 出发的环岛航行为一条满足以下条件的路径： - 路径的起点和终点都是 $(x, y)$。 - 如果 Thomas 当前在格子 $(i, j)$，他可以移动到 $(i+1, j)$、$(i-1, j)$、$(i, j-1)$、$(i, j+1)$，只要目标格子是海洋格子或海底火山格子且仍在网格内。注意，在一次环岛航行中允许多次经过同一个格子。 - 路径必须环绕岛屿并完全包围它。某条路径 $p$ 完全包围岛屿，指的是如果不经过路径 $p$ 上的格子，仅通过相邻（包括对角线相邻）的格子移动，则无法从任意岛屿格子到达网格边界。下图中，从 $(2, 2)$ 出发，经过 $(1, 3)$，再以另一条路返回 $(2, 2)$ 的路径并未完全包围岛屿，因此不算作一次环岛航行。 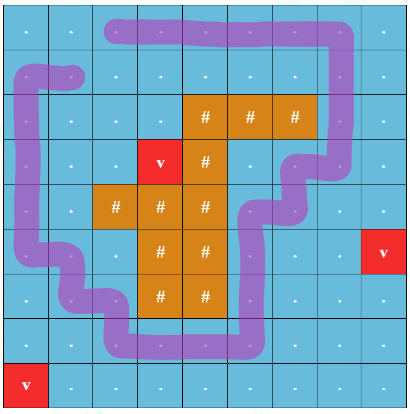 未完全包围岛屿的路径示例 一次环岛航行的安全性定义为：路径上某个格子到最近海底火山的曼哈顿距离 $^{\ddagger}$ 的最小值（注意岛屿格子的存在不影响该距离）。 你有 $q$ 次询问。每次询问为 $(x, y)$，你需要求出从 $(x, y)$ 出发的环岛航行的最大安全性。保证 $(x, y)$ 是海洋格子或海底火山格子。 $^{\dagger}$ 一组格子构成一个连通块，指的是从该组任意一个格子出发，只通过该组内的格子且每次移动到有公共边的相邻格子，可以到达该组内的任意一个格子。 $^{\ddagger}$ 格子 $(r_1, c_1)$ 和 $(r_2, c_2)$ 的曼哈顿距离为 $|r_1 - r_2| + |c_1 - c_2|$。

第一行包含三个整数 $n$、$m$ 和 $q$（$3 \leq n, m \leq 10^5$，$9 \leq n \cdot m \leq 3 \cdot 10^5$，$1 \leq q \leq 3 \cdot 10^5$），分别表示网格的行数、列数和询问数。 接下来的 $n$ 行，每行包含 $m$ 个字符，描述网格中的格子。'\#' 表示岛屿格子，'.' 表示海洋格子，'v' 表示海底火山格子。 保证至少有一个岛屿格子和至少有一个海底火山格子。保证所有岛屿格子构成一个连通块，所有海洋格子和海底火山格子构成一个连通块。并且保证网格边界上没有岛屿格子。 接下来的 $q$ 行，每行包含两个整数 $x$ 和 $y$（$1 \leq x \leq n$，$1 \leq y \leq m$），表示一次从 $(x, y)$ 出发的环岛航行。 保证 $(x, y)$ 是海洋格子或海底火山格子。

对于每个询问，输出一个整数，表示从指定位置出发的环岛航行的最大安全性。

对于第一个示例，下图展示了从 $(1, 1)$ 出发的最优环岛航行。该环岛航行的安全性为 $3$，因为路径上某个格子到最近海底火山的曼哈顿距离的最小值为 $3$。 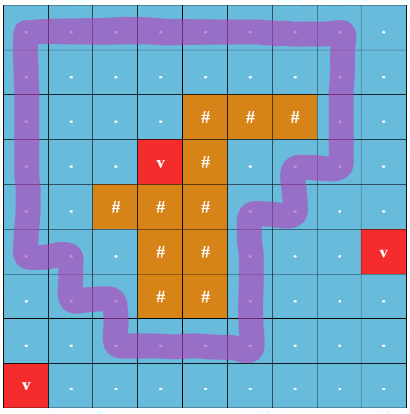 最优环岛航行示例 对于第四个示例，注意在一次环岛航行中允许多次经过同一个格子。例如，从 $(7, 6)$ 出发的环岛航行就必须多次经过同一个格子。 由 ChatGPT 4.1 翻译