CF1921E Eat the Chip

Alice 和 Bob 正在一个棋盘上玩游戏。棋盘有 $h$ 行，从上到下编号，有 $w$ 列，从左到右编号。两位玩家各有一个棋子。最开始，Alice 的棋子位于坐标 $(x_a, y_a)$（第 $x_a$ 行，第 $y_a$ 列），Bob 的棋子位于 $(x_b, y_b)$。保证两枚棋子的初始位置不会重合。两位玩家轮流行动，Alice 先手。 在她的回合，Alice 可以将她的棋子移动到正下方、左下方或右下方的相邻格子。Bob 则可以将他的棋子移动到正上方、左上方或右上方的相邻格子。棋子不能移动到棋盘之外。 更具体地说，如果 Alice 的回合开始时她在 $(x_a, y_a)$，她可以将棋子移动到 $(x_a + 1, y_a)$、$(x_a + 1, y_a - 1)$ 或 $(x_a + 1, y_a + 1)$。Bob 的回合，如果他在 $(x_b, y_b)$，他可以将棋子移动到 $(x_b - 1, y_b)$、$(x_b - 1, y_b - 1)$ 或 $(x_b - 1, y_b + 1)$。新的棋子坐标 $(x', y')$ 必须满足 $1 \le x' \le h$ 且 $1 \le y' \le w$。 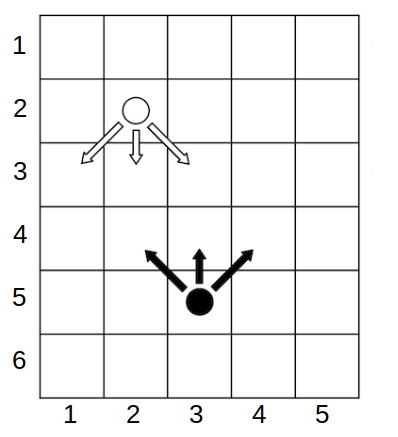 示例游戏状态。Alice 用白色棋子，Bob 用黑色棋子。箭头表示可能的移动。若某位玩家将棋子移动到对方棋子所在的格子，则立即获胜。如果某位玩家无法行动（Alice 到达最后一行，即 $x_a = h$，Bob 到达第一行，即 $x_b = 1$），则游戏立即以平局结束。 如果双方都采取最优策略，游戏结果会如何？

每组测试数据包含多组测试用例。第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。接下来是每组测试用例的描述。 每组测试用例包含一行六个整数 $h$、$w$、$x_a$、$y_a$、$x_b$、$y_b$（$1 \le x_a, x_b \le h \le 10^6$，$1 \le y_a, y_b \le w \le 10^9$），分别表示棋盘的尺寸以及 Alice 和 Bob 的初始位置。保证 $x_a \ne x_b$ 或 $y_a \ne y_b$。 保证所有测试用例中 $h$ 的总和不超过 $10^6$。

对于每组测试用例，输出一行，内容为 "Alice"（如果 Alice 获胜）、"Bob"（如果 Bob 获胜）或 "Draw"（如果双方都无法获胜）。输出大小写不敏感，例如 "bOb"、"bob"、"Bob" 和 "BOB" 都视为 Bob 获胜。

由 ChatGPT 4.1 翻译