CF1921G Mischievous Shooter

Once the mischievous and wayward shooter named Shel found himself on a rectangular field of size $ n \times m $ , divided into unit squares. Each cell either contains a target or not. Shel only had a lucky shotgun with him, with which he can shoot in one of the four directions: right-down, left-down, left-up, or right-up. When fired, the shotgun hits all targets in the chosen direction, the Manhattan distance to which does not exceed a fixed constant $ k $ . The Manhattan distance between two points $ (x_1, y_1) $ and $ (x_2, y_2) $ is equal to $ |x_1 - x_2| + |y_1 - y_2| $ . 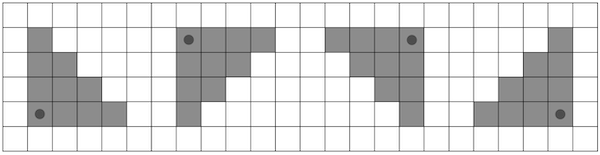 Possible hit areas for $ k = 3 $ .Shel's goal is to hit as many targets as possible. Please help him find this value.

Each test consists of several test cases. The first line contains a single integer $ t $ ( $ 1 \le t \le 1000 $ ) — the number of test cases. Then follows the description of the test cases. The first line of each test case contains field dimensions $ n $ , $ m $ , and the constant for the shotgun's power $ k $ ( $ 1 \le n, m, k \le 10^5, 1 \le n \cdot m \le 10^5 $ ). Each of the next $ n $ lines contains $ m $ characters — the description of the next field row, where the character '.' means the cell is empty, and the character '\#' indicates the presence of a target. It is guaranteed that the sum of $ n \cdot m $ over all test cases does not exceed $ 10^5 $ .

For each test case, output a single integer on a separate line, which is equal to the maximum possible number of hit targets with one shot.

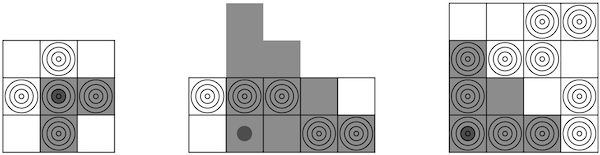
Possible optimal shots for the examples in the statement: