CF1924C Fractal Origami

你有一张边长为 $1$ 单位的正方形纸。在一次操作中，你将正方形的每个角折向纸的中心，从而形成另一个边长为 $\dfrac{1}{\sqrt{2}}$ 单位的正方形。以这个新正方形为基础，你再次进行相同的操作，并重复这个过程共 $N$ 次。 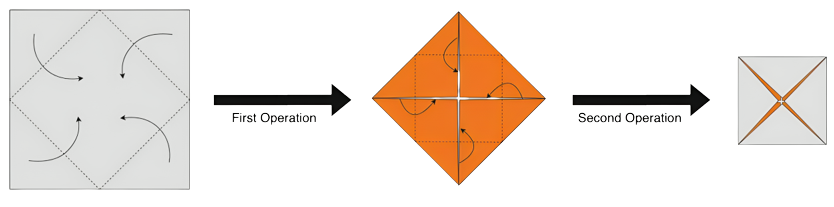 对 $N=2$ 进行操作的过程。 完成所有操作后，你将纸张展开，并保持最初的那一面朝上，此时纸上会出现一些折痕。每一条折痕都属于两种类型之一：山折或谷折。山折是指纸向外折，谷折是指纸向内折。 你计算所有山折痕的总长度，记为 $M$。同理，计算所有谷折痕的总长度，记为 $V$。你想要计算 $\dfrac{M}{V}$ 的值。 可以证明，这个值可以表示为 $A+B\sqrt{2}$ 的形式，其中 $A$ 和 $B$ 是有理数。设 $B$ 可以表示为最简分数 $\dfrac{p}{q}$，你的任务是输出 $p \times inv(q)$ 对 $999\,999\,893$ 取模的结果（注意这是一个非常规的模数），其中 $inv(q)$ 表示 $q$ 关于 $999\,999\,893$ 的[模逆元](https://en.wikipedia.org/wiki/Modular_multiplicative_inverse)。

每组测试数据包含多个测试用例。第一行包含测试用例个数 $t$（$1 \leq t \leq 10^4$）。 接下来每个测试用例一行，包含一个整数 $N$（$1 \leq N \leq 10^9$），表示你对正方形纸张进行的操作次数。

对于每个测试用例，输出一行答案。

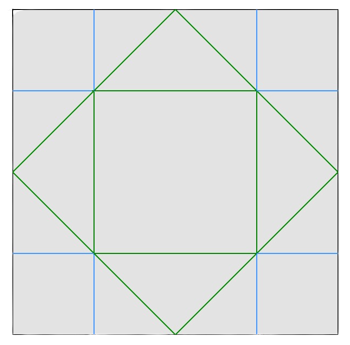
下图中，蓝色线条表示山折痕，绿色线条表示谷折痕。  经过 $1$ 次操作后的折痕（$\dfrac{M}{V}=0$）。 经过 $2$ 次操作后的折痕（$\dfrac{M}{V}=\sqrt{2}-1$）。 由 ChatGPT 4.1 翻译