CF1926G Vlad and Trouble at MIT

Vladislav 有一个儿子，非常想去 MIT。MIT（摩尔多瓦理工学院）的学生宿舍可以用一棵有 $n$ 个顶点的树来表示，每个顶点代表一个房间，且每个房间里正好有一名学生。一棵树是一个有 $n$ 个顶点和 $n-1$ 条边的连通无向图。 今晚有三类学生： - 想要开派对并播放音乐的学生（用 $\texttt{P}$ 标记）； - 想要睡觉并享受安静的学生（用 $\texttt{S}$ 标记）； - 不在乎的学生（用 $\texttt{C}$ 标记）。 最初，所有的边都是薄墙，音乐可以穿透薄墙传播，所以当某个开派对的学生播放音乐时，所有房间都能听到。然而，我们可以在任意边上安装厚墙——厚墙可以阻挡音乐的传播。 学校希望安装一些厚墙，使得每个开派对的学生都能播放音乐，但没有任何想睡觉的学生能听到音乐。 由于学校在冠名权诉讼中损失了大量资金，他们希望你帮忙计算需要使用的最少厚墙数量。

第一行包含一个整数 $t$（$1 \leq t \leq 1000$），表示测试用例的数量。 每个测试用例的第一行包含一个整数 $n$（$2 \leq n \leq 10^5$），表示树的顶点数。 每个测试用例的第二行包含 $n-1$ 个整数 $a_2, \dots, a_n$（$1 \leq a_i < i$），表示在树中第 $i$ 个顶点与 $a_i$ 之间有一条边。 每个测试用例的第三行包含一个长度为 $n$ 的字符串 $s$，由字符 $\texttt{P}$、$\texttt{S}$ 和 $\texttt{C}$ 组成，表示第 $i$ 个学生的类型为 $s_i$。 所有测试用例中 $n$ 的总和不超过 $10^5$。

对于每个测试用例，输出一个整数，表示需要安装的最少厚墙数量。

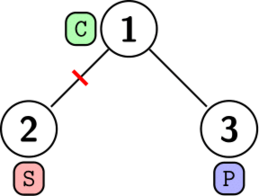
在第一个样例中，我们可以在房间 $1$ 和 $2$ 之间安装一堵厚墙，如下图所示。不能不安装墙，否则房间 $3$ 的音乐会传到房间 $2$，而房间 $2$ 的学生想要睡觉，所以答案是 $1$。当然，也存在其他可行方案。  由 ChatGPT 4.1 翻译