CF1928F Digital Patterns

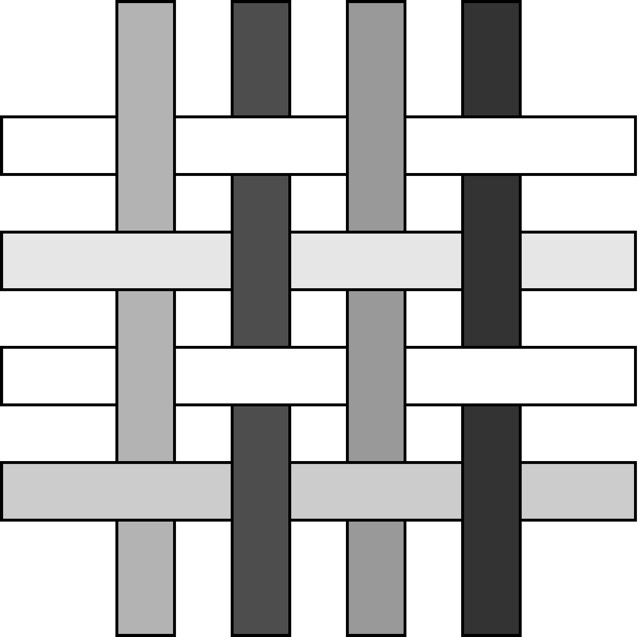
Anya 正在进行针线活。今天她决定用半透明的线织一条围巾。每根线都有一个整数表示的透明度系数。 围巾的制作方式如下：选择透明度系数为 $a_1, a_2, \ldots, a_n$ 的横向线和透明度系数为 $b_1, b_2, \ldots, b_m$ 的纵向线。然后如图所示将它们交织在一起，形成一个大小为 $n \times m$ 的织物片段，共有 $nm$ 个节点：  $n = m = 4$ 时的织物片段示例。 当交织收紧且线之间没有缝隙时，每个由第 $i$ 根横向线和第 $j$ 根纵向线形成的节点会变成一个格子，记作 $(i, j)$。格子 $(i, j)$ 的透明度系数为 $a_i + b_j$。 最终围巾的“有趣度”定义为其所有子正方形 $^\dagger$ 中，不存在有相邻 $^{\dagger\dagger}$ 格子透明度系数相同的子正方形的个数。 Anya 还没有决定使用哪些线，所以你还会得到 $q$ 个关于线透明度系数区间加减的操作请求。每次操作后，你需要输出当前围巾的有趣度。 $^\dagger$ 织物片段的子正方形定义为：所有满足 $x_0 \le i \le x_0 + d$ 且 $y_0 \le j \le y_0 + d$ 的格子 $(i, j)$ 的集合，其中 $x_0, y_0, d$ 为整数，$1 \le x_0 \le n - d$，$1 \le y_0 \le m - d$，$d \ge 0$。 $^{\dagger\dagger}$ 格子 $(i_1, j_1)$ 和 $(i_2, j_2)$ 相邻，当且仅当 $|i_1 - i_2| + |j_1 - j_2| = 1$。

第一行包含三个整数 $n$、$m$ 和 $q$（$1 \le n, m \le 3 \cdot 10^5$，$0 \le q \le 3 \cdot 10^5$）——横向线的数量、纵向线的数量和操作请求的数量。 第二行包含 $n$ 个整数 $a_1, a_2, \ldots, a_n$（$-10^9 \le a_i \le 10^9$）——横向线的透明度系数，线从上到下编号。 第三行包含 $m$ 个整数 $b_1, b_2, \ldots, b_m$（$-10^9 \le b_i \le 10^9$）——纵向线的透明度系数，线从左到右编号。 接下来的 $q$ 行，每行描述一个操作请求。每个请求由四个整数 $t$、$l$、$r$、$x$ 组成（$1 \le t \le 2$，$l \le r$，$-10^9 \le x \le 10^9$）。根据 $t$ 的值，操作如下： - $t=1$：将横向线区间 $[l, r]$ 的透明度系数都增加 $x$（即对所有 $l \le i \le r$，$a_i$ 增加 $x$）； - $t=2$：将纵向线区间 $[l, r]$ 的透明度系数都增加 $x$（即对所有 $l \le i \le r$，$b_i$ 增加 $x$）。

输出 $q+1$ 行。第 $i+1$ 行（$0 \le i \le q$）输出一个整数，表示前 $i$ 次操作后围巾的有趣度。

在第一个样例中，最终织物片段中各格子的透明度系数如下： 2334 2334 3445 4556 其中，不包含有相邻格子透明度系数相同的子正方形有： - 每个单独的 $16$ 个格子； - 以 $(3, 1)$ 为左上角、$(4, 2)$ 为右下角的子正方形； - 以 $(2, 3)$ 为左上角、$(3, 4)$ 为右下角的子正方形； - 以 $(2, 1)$ 为左上角、$(3, 2)$ 为右下角的子正方形； - 以 $(3, 3)$ 为左上角、$(4, 4)$ 为右下角的子正方形。 在第二个样例中，第一次操作后横向线的透明度系数为 $[1, 2, 2]$。第二次操作后纵向线的透明度系数为 $[2, -4, 2]$。 由 ChatGPT 4.1 翻译