CF1929B Sasha and the Drawing
题目描述
即使在幼儿园,Sasha 也喜欢一个女孩。因此,他想给她一幅画,并吸引她的注意力。
作为绘画,他决定绘制一个大小为 $n\times n$ 的正方形网格,其中染色的一些单元格。但是着色单元格很困难,因此他希望尽可能少地染色。但与此同时,他希望至少有 $k$ 条对角线至少有一个染色单元格。注意,大小为 $n \times n$ 的正方形网格总共有 $4n - 2$ 条对角线。
帮助小 Sasha 让女孩爱上他,并告诉他需要染色的最少单元格数。
输入格式
每个测试用例包括多个测试。第一行包含一个整数 $t$($1 \le t \le 1000$)——测试用例数。接下来是描述测试用例。
每个测试用例的唯一行包含两个整数 $n$ 和 $k$($2 \leq n \leq 10^8$,$1 \leq k \leq 4n - 2$)——正方形网格的大小和至少应包含一个染色单元格的对角线数。
输出格式
对于每个测试用例,输出一个整数——需要染色的最少单元格数。
### 样例
#### 输入样例:
```
7
3 4
3 3
3 10
3 9
4 7
7 11
2 3
```
#### 输出样例:
```
2
2
6
5
4
6
2
```
说明/提示
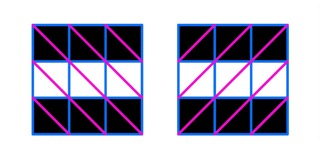
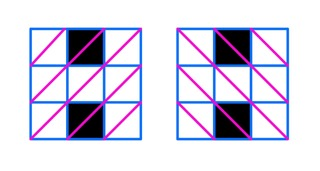
下面的图片中,黑色标记染色单元格,所有对角线标记为紫色。
在第一个测试用例中,您可以染色 $2$ 个单元格,以使 $4$ 条对角线包含至少一个染色单元格。
在第三个测试用例中,您可以染色 $6$ 个单元格,以使所有 $10$ 条对角线都包含至少一个染色单元格。