CF1929D Sasha and a Walk in the City
题目描述
Sasha 想和他的女友在城市中散步。该城市由 $n$ 个路口组成,编号为 $1$ 到 $n$ 。它们中的某些被道路连接,从任何一个路口出发,都可以恰好通向任何其他路口,换句话说,这些路口和它们之间的道路组成了一棵树。
其中有一些路口被认为很危险。由于在城市中独自走路是不安全的,所以 Sasha 不想在散步时经过三个或更多的危险路口。
Sasha 认为,一组路口如果满足以下条件则称它为好的:
- 如果在城市中只有这组路口中的路口是危险的,那么城市中的任何简单路径都包含不超过两个危险路口。
然而,Sasha 并不知道哪些路口是危险的,因此他对城市中不同好的路口组合的数量感兴趣。由于这个数量可能很大,输出其模数为 $998244353$ 的值。
简单路径是指最多经过每个路口一次的路径。
输入格式
每个测试包含多个测试用例。第一行包含一个整数 $t$ ($1\le t\le 10^4$) —— 测试用例的数量。接下来是对于每个测试用例的描述:
每个测试用例的第一行包含一个整数 $n$ ($2\le n\le 3\times 10^5$) —— 城市中的路口数。
接下来 $n-1$ 行描述了这些道路。其中第 $i$ 行包含两个整数 $u_i$ 和 $v_i$ ($1\le u_i,v_i\le n, u_i\neq v_i$) 代表一条连接 $u_i$ 和 $v_i$ 的道路。
保证这些道路形成一棵树。
保证所有测试用例中 $n$ 的总和不超过 $3\times 10^5$。
输出格式
对于每个测试用例,输出一个整数,即合法路口集合的数量对 $998244353$ 取模的结果。
说明/提示
在第一个测试用例中,有 $2^3=8$ 个集合是可以选的。除了集合 $\{1,2,3\}$ 以外的集合都是好的,因为如果在城市中只有 $\{1,2,3\}$ 中的路口是危险的,那么路口 $1,2,3$ 对应的道路构成的简单路径 $1-2-3$ 包含了 $3$ 个危险路口。因此,一共有 $7$ 个合法路口集合。
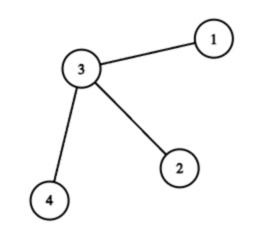
在第二个测试用例中,有 $2^4=16$ 个集合是可以选的,但是其中 $\{1,2,3,4\}, \{1,2,3\},\{1,3,4\},\{2,3,4\}$ 不是合法的集合。因此一共有 $16-4=12$ 个合法路口集合。城市分布如下图所示: