CF1933F Turtle Mission: Robot and the Earthquake

这个世界是一个有 $n$ 行 $m$ 列的网格。行编号为 $0, 1, \ldots, n-1$，列编号为 $0, 1, \ldots, m-1$。在这个世界中，列是循环的（即每一列的最上方和最下方的格子是相邻的）。第 $i$ 行第 $j$ 列的格子（$0 \le i < n, 0 \le j < m$）记作 $(i,j)$。 在时间 $0$ 时，格子 $(i,j)$（$0 \le i < n, 0 \le j < m$）中可能有一块石头，也可能什么都没有。格子 $(i,j)$ 的状态可以用整数 $a_{i,j}$ 描述： - 如果 $a_{i,j} = 1$，则 $(i,j)$ 处有一块石头。 - 如果 $a_{i,j} = 0$，则 $(i,j)$ 处没有石头。 由于地震的余震，所有列会像板块运动一样循环向上移动，每单位时间每列向上移动 $1$ 格。具体来说，对于某个 $0 \le i < n, 0 \le j < m$，如果 $(i,j)$ 此时有一块石头，它会从 $(i, j)$ 移动到 $(i-1, j)$（如果 $i=0$，则移动到 $(n-1, j)$）。 机器人 RT 初始位于 $(0,0)$。它需要前往 $(n-1,m-1)$ 执行地震救援任务（即右下角的格子）。地震不会改变机器人的位置，只会改变石头的位置。 设 RT 当前位于 $(x,y)$（$0 \le x < n, 0 \le y < m$），它可以执行以下操作： - 循环向上移动一格，即从 $(x,y)$ 移动到 $((x+n-1) \bmod n, y)$，耗时 $1$ 单位时间。 - 循环向下移动一格，即从 $(x,y)$ 移动到 $((x+1) \bmod n, y)$，耗时 $1$ 单位时间。 - 向右移动一格，即从 $(x,y)$ 移动到 $(x, y+1)$，耗时 $1$ 单位时间。（仅当 $y < m-1$ 时可以执行此操作。） 注意，RT 不能向左移动，也不能停留在原地。 不幸的是，如果 RT 与石头相撞会爆炸。因此，当 RT 位于 $(x,y)$ 时，如果 $((x+1) \bmod n, y)$ 或 $((x+2) \bmod n, y)$ 有石头，RT 不能向下移动，否则会被石头击中。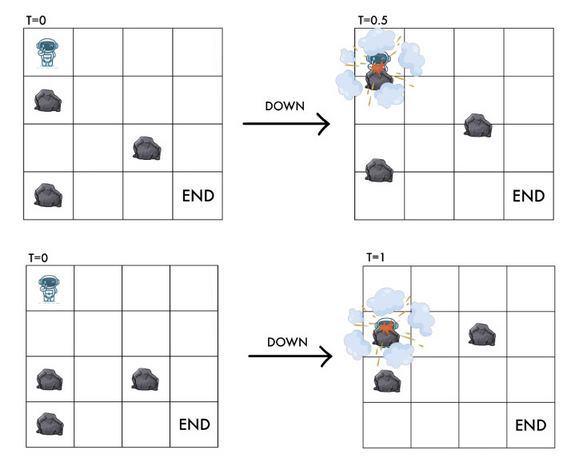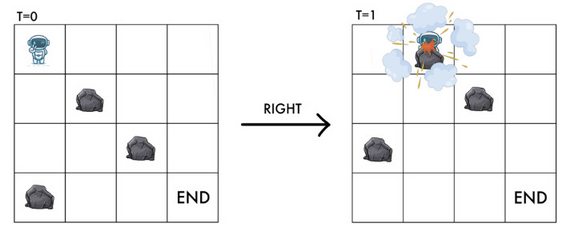  同样地，如果 $y+1 < m$ 且 $((x+1) \bmod n, y+1)$ 有石头，RT 不能向右移动，否则会被石头击中。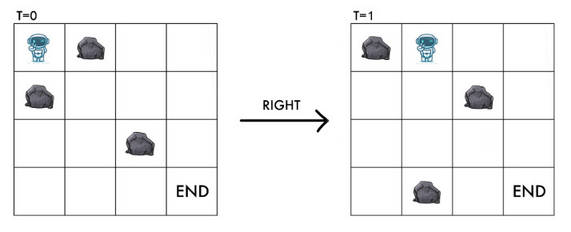  但需要注意的是，如果 $(x \bmod n, y+1)$ 和 $((x+1) \bmod n, y)$ 都有石头，RT 依然可以安全地向右移动。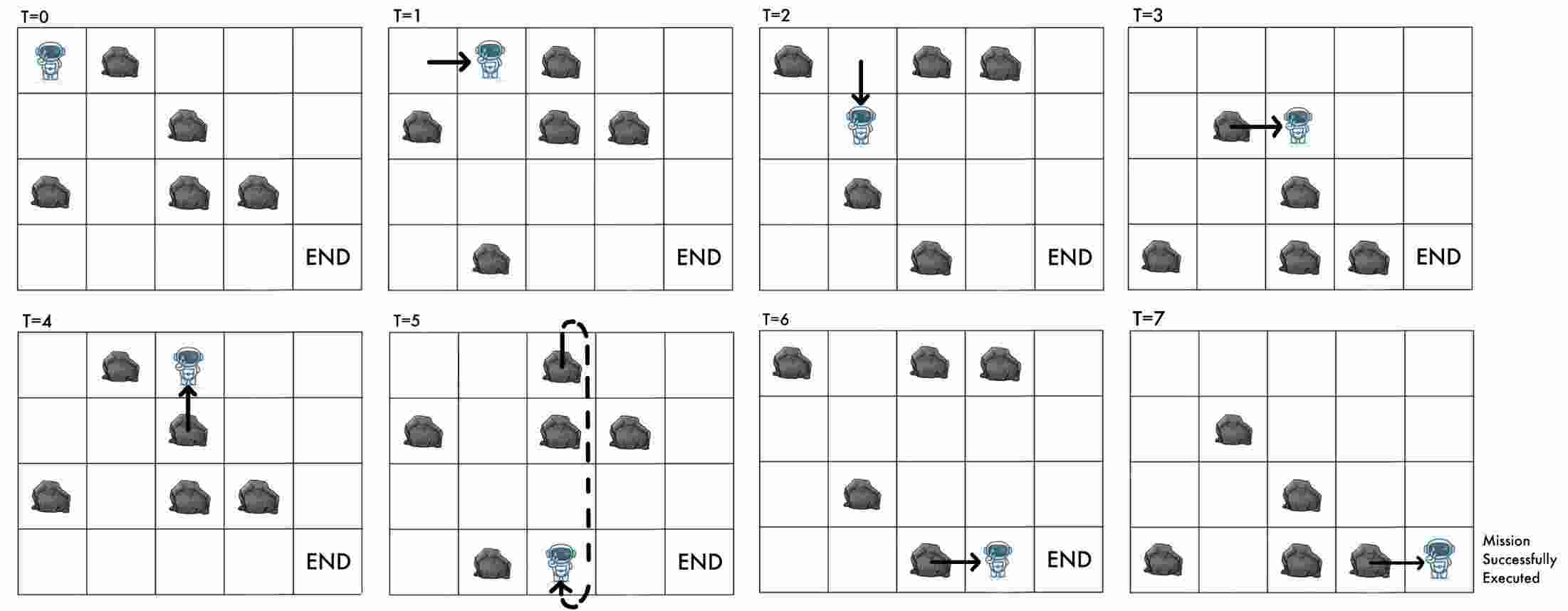  请你计算 RT 到达 $(n-1,m-1)$ 且不与任何石头相撞所需的最少时间。如果无法到达，输出 $-1$。

输入的第一行包含一个整数 $t$（$1 \le t \le 10^4$），表示测试用例的数量。 每个测试用例的第一行包含两个整数 $n$、$m$（$3 \le n, m \le 10^3$），表示星球的边界大小。 接下来的 $n$ 行，每行包含 $m$ 个整数。第 $(i+1)$ 行第 $(j+1)$ 个整数（$0 \le i < n, 0 \le j < m$）为 $a_{i,j}$，表示在时间 $0$ 时 $(i,j)$ 是否有石头。 另外，保证 $a_{0,0} = 0$，且对于 $0 \le i < n$，$a_{i, m-1} = 0$。也就是说，RT 的初始位置以及第 $m-1$ 列都没有石头。 所有测试用例中 $n \cdot m$ 的总和不超过 $10^6$。

对于每个测试用例： - 如果可以在不与任何石头相撞的情况下到达终点，输出一个整数——RT 到达 $(n-1,m-1)$ 所需的最少时间。 - 否则，输出 $-1$。

下图为样例第一个测试用例的可视化说明：  由 ChatGPT 4.1 翻译