CF1935F Andrey's Tree
题目描述
安德烈大师非常喜欢树$^{\dagger}$,所以他拥有一棵包含 $n$ 个顶点的树。
但事情并不简单。提莫菲大师决定从树中偷走一个顶点。如果提莫菲从树中移除顶点 $v$,那么顶点 $v$ 以及所有与 $v$ 相连的边都会被从树中移除,其他顶点的编号保持不变。为了不让安德烈伤心,提莫菲决定让剩下的图再次成为一棵树。为此,他可以在任意两个顶点 $a$ 和 $b$ 之间添加边,但每添加一条边,他都需要向大师援助中心支付 $|a-b|$ 个金币。
注意,最终得到的树中不包含顶点 $v$。
提莫菲还没有决定要移除哪个顶点 $v$,所以他想知道对于每个顶点 $1 \leq v \leq n$,在移除顶点 $v$ 后,为了让图再次成为一棵树,所需花费的最少金币数,以及需要添加哪些边。
$^{\dagger}$ 一棵树是一个无向连通且无环的图。
输入格式
每组测试数据包含多组测试用例。第一行包含一个整数 $t$($1 \leq t \leq 10^4$)——表示测试用例的数量。接下来是每组测试用例的描述。
每组测试用例的第一行包含一个整数 $n$($5 \leq n \leq 2 \cdot 10^5$)——表示安德烈的树的顶点数。
接下来的 $n-1$ 行,每行包含两个整数 $u_i$ 和 $v_i$($1 \leq u_i, v_i \leq n$),表示树中的一条边连接了顶点 $u_i$ 和 $v_i$。
保证给定的边构成一棵树。
保证所有测试用例中 $n$ 的总和不超过 $2 \cdot 10^5$。
输出格式
对于每组测试用例,按如下格式输出答案:
对于每个顶点 $v$(按 $1$ 到 $n$ 的顺序),第一行输出两个整数 $w$ 和 $m$——表示移除顶点 $v$ 后,为了让图再次成为一棵树所需花费的最少金币数,以及需要添加的边的数量。
接下来输出 $m$ 行,每行包含两个整数 $a$ 和 $b$($1 \leq a, b \leq n, a \ne v, b \ne v, a \ne b$),表示需要添加的边的两个端点。
如果有多种添加边的方式,只需输出任意一种最小花费的方案即可。
说明/提示
在第一个测试用例中:
考虑移除顶点 $4$:
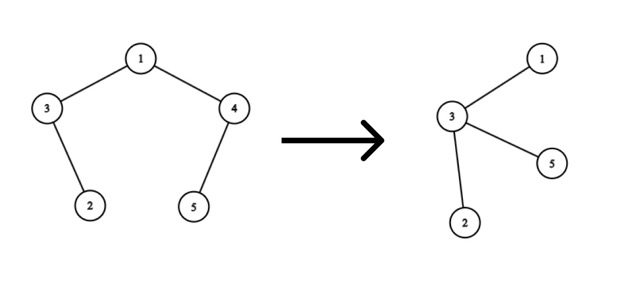 最优方案是添加一条从顶点 $5$ 到顶点 $3$ 的边。这样我们将花费 $|5-3|=2$ 个金币。
在第三个测试用例中:
考虑移除顶点 $1$:
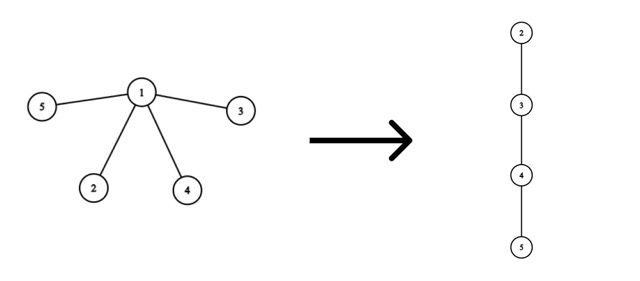 最优方案如下:
- 添加一条从顶点 $2$ 到顶点 $3$ 的边,花费 $|2-3|=1$ 个金币。
- 添加一条从顶点 $3$ 到顶点 $4$ 的边,花费 $|3-4|=1$ 个金币。
- 添加一条从顶点 $4$ 到顶点 $5$ 的边,花费 $|4-5|=1$ 个金币。
这样总共花费 $1+1+1=3$ 个金币。
考虑移除顶点 $2$:
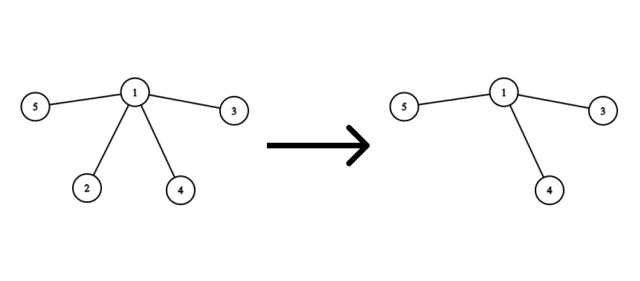 不需要添加任何边,因为移除该顶点后图仍然是一棵树。
由 ChatGPT 4.1 翻译