CF1935F Andrey's Tree

Master Andrey loves trees $ ^{\dagger} $ very much, so he has a tree consisting of $ n $ vertices. But it's not that simple. Master Timofey decided to steal one vertex from the tree. If Timofey stole vertex $ v $ from the tree, then vertex $ v $ and all edges with one end at vertex $ v $ are removed from the tree, while the numbers of other vertices remain unchanged. To prevent Andrey from getting upset, Timofey decided to make the resulting graph a tree again. To do this, he can add edges between any vertices $ a $ and $ b $ , but when adding such an edge, he must pay $ |a - b| $ coins to the Master's Assistance Center. Note that the resulting tree does not contain vertex $ v $ . Timofey has not yet decided which vertex $ v $ he will remove from the tree, so he wants to know for each vertex $ 1 \leq v \leq n $ , the minimum number of coins needed to be spent to make the graph a tree again after removing vertex $ v $ , as well as which edges need to be added. $ ^{\dagger} $ A tree is an undirected connected graph without cycles.

Each test consists of multiple test cases. The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 5 \le n \le 2\cdot10^5 $ ) — the number of vertices in Andrey's tree. The next $ n - 1 $ lines contain a description of the tree's edges. The $ i $ -th of these lines contains two integers $ u_i $ and $ v_i $ ( $ 1 \le u_i, v_i \le n $ ) — the numbers of vertices connected by the $ i $ -th edge. It is guaranteed that the given edges form a tree. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2\cdot10^5 $ .

For each test case, output the answer in the following format: For each vertex $ v $ (in the order from $ 1 $ to $ n $ ), in the first line output two integers $ w $ and $ m $ — the minimum number of coins that need to be spent to make the graph a tree again after removing vertex $ v $ , and the number of added edges. Then output $ m $ lines, each containing two integers $ a $ and $ b $ ( $ 1 \le a, b \le n, a \ne v, b \ne v $ , $ a \ne b $ ) — the ends of the added edge. If there are multiple ways to add edges, you can output any solution with the minimum cost.

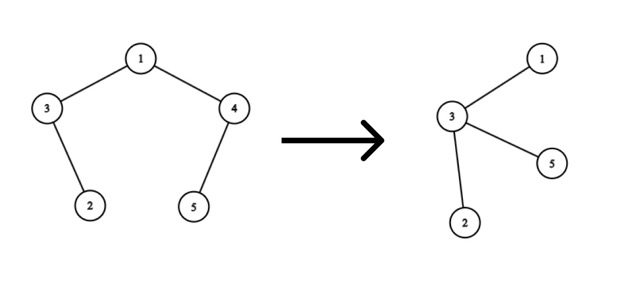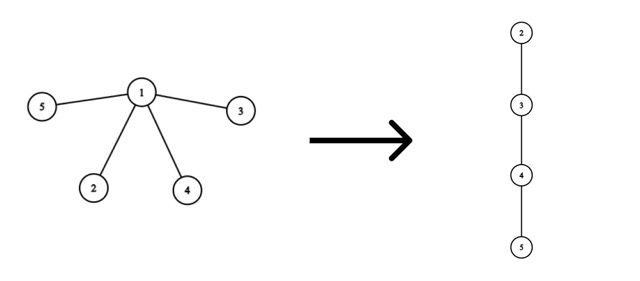In the first test case: Consider the removal of vertex $ 4 $ : The optimal solution would be to add an edge from vertex $ 5 $ to vertex $ 3 $ . Then we will spend $ |5 - 3| = 2 $ coins. In the third test case: Consider the removal of vertex $ 1 $ : The optimal solution would be: - Add an edge from vertex $ 2 $ to vertex $ 3 $ , spending $ |2 - 3| = 1 $ coin. - Add an edge from vertex $ 3 $ to vertex $ 4 $ , spending $ |3 - 4| = 1 $ coin. - Add an edge from vertex $ 4 $ to vertex $ 5 $ , spending $ |4 - 5| = 1 $ coin. Then we will spend a total of $ 1 + 1 + 1 = 3 $ coins. 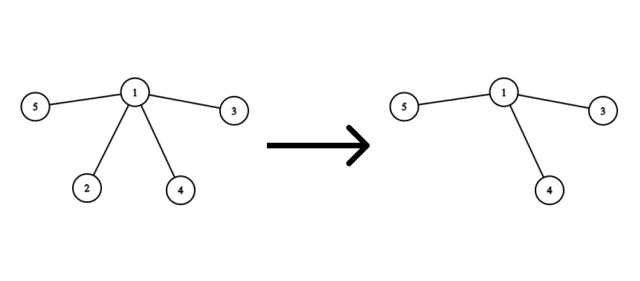Consider the removal of vertex $ 2 $ : No edges need to be added, as the graph will remain a tree after removing the vertex.