CF1936F Grand Finale: Circles
题目描述
平面上有 $n$ 个圆 $(x_i,y_i,r_i)$,其中 $(x_i,y_i)$ 是第 $i$ 个圆的圆心坐标,$r_i$ 是第 $i$ 个圆的半径。你需要找到满足以下条件的圆 $C$:
- $C$ 被 $n$ 个圆的**交集**包含。或者说,$C$ 内含或内切于每一个圆中。
- $C$ 是满足上个条件的圆中,半径最大的。
若正确的半径为 $a$,你输出的描述 $C$ 的三元组为 $(x,y,r)$,你的答案会被接受当且仅当:
- 对于每一个 $i$,$\sqrt{(x_i-x)^2+(y_i-y)^2}+r\le r_i+\max(a,1)\cdot10^{-7}$.
- $r$ 的绝对误差或相对误差不超过 $10^{-7}$。形式化地,你的答案会被接受当且仅当 $\frac{\lvert r-a\rvert}{\max(a,1)}$.
输入格式
第一行一个正整数 $n(1\le n\le 10^5)$,表示圆的个数。
接下来的 $n$ 行中,第 $i$ 行包含三个整数 $x_i,y_i,r_i(-10^6\le x_i,y_i\le 10^6,1\le r_i\le 2\cdot 10^6)$。
数据保证存在一个半径不小于 $10^{-6}$ 的圆被包含于给定圆的交集中。
输出格式
输出一行共三个实数 $x,y,r$,表示 $C$ 的圆心坐标为 $(x,y)$,半径为 $r$。
说明/提示
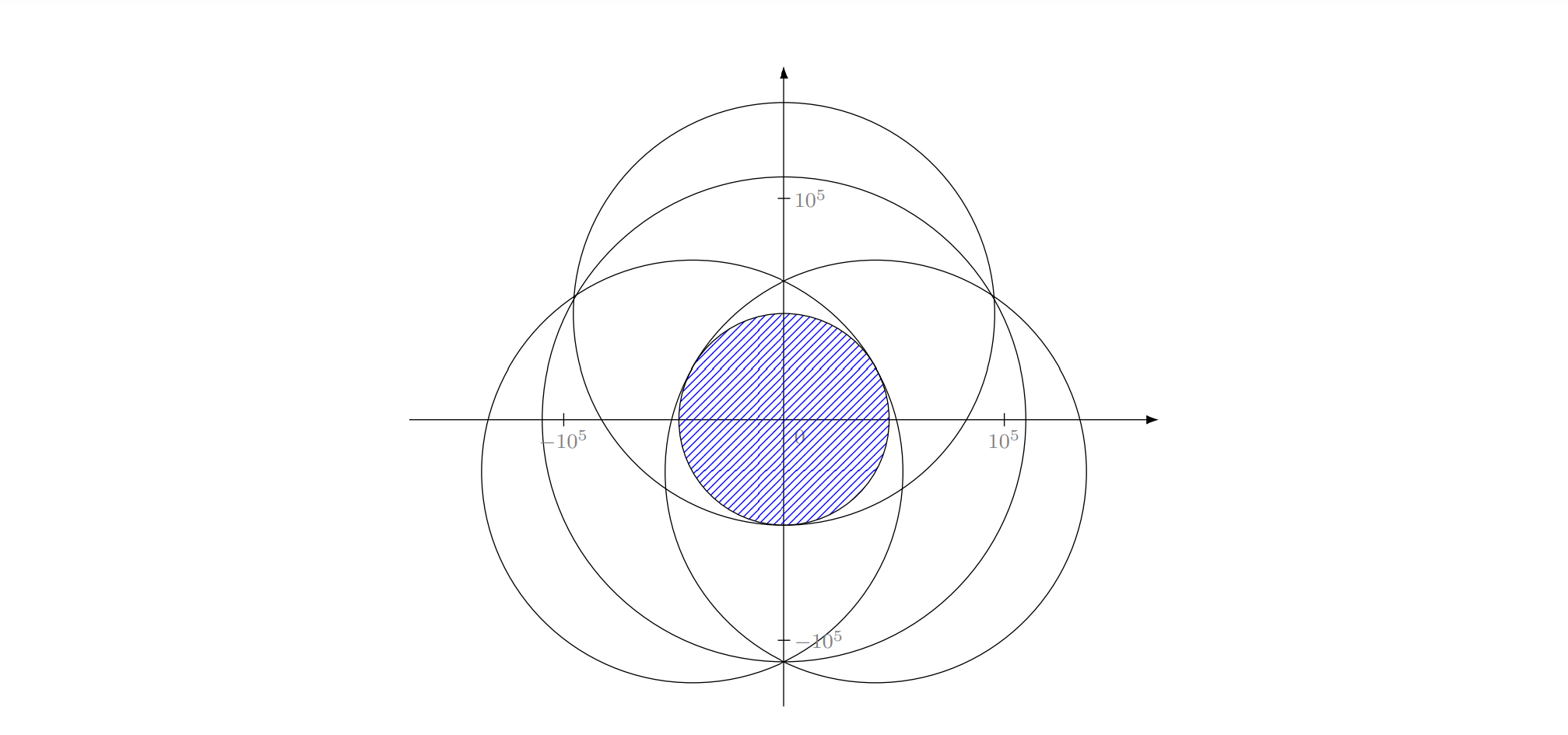
A two-dimensional plot depicting the first test case is given below. The output circle $ C $ is dashed with blue lines.
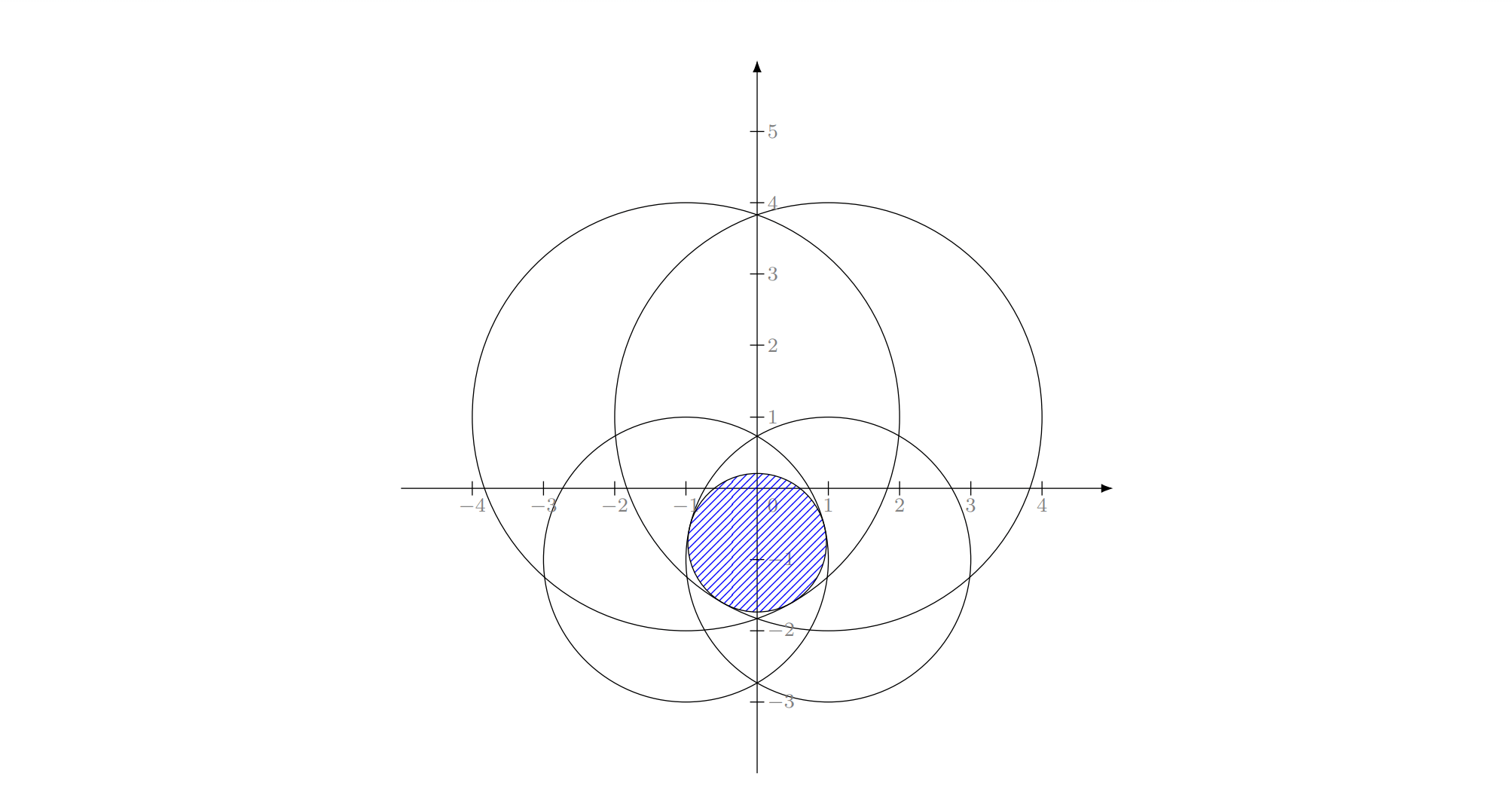A two-dimensional plot depicting the second test case is given below. The output circle $ C $ is dashed with blue lines.