CF1936F Grand Finale: Circles

You are given $ n $ circles on the plane. The $ i $ -th of these circles is given by a tuple of integers $ (x_i, y_i, r_i) $ , where $ (x_i, y_i) $ are the coordinates of its center, and $ r_i $ is the radius of the circle. Please find a circle $ C $ which meets the following conditions: - $ C $ is contained inside all $ n $ circles given in the input. - Among all circles $ C $ that meet the first condition, the radius of the circle is maximum. Let the largest suitable circle have the radius of $ a $ . Your output $ C $ , described as $ (x,y,r) $ , will be accepted if it meets the following conditions: - For each $ i $ , $ \sqrt{(x_i-x)^2+(y_i-y)^2}+ r \le r_i+\max(a,1)\cdot 10^{-7} $ . - The absolute or relative error of $ r $ does not exceed $ 10^{-7} $ . Formally, your answer is accepted if and only if $ \frac{\left|r - a\right|}{\max(1, a)} \le 10^{-7} $ .

The first line contains a single integer $ n $ ( $ 1 \le n \le 10^5 $ ) — the number of circles. The $ i $ -th of the following $ n $ lines contains three integers $ x_i $ , $ y_i $ , $ r_i $ ( $ -10^6 \le x_i,y_i \le 10^6 $ , $ 1 \le r_i \le 2 \cdot 10^6 $ ). It is guaranteed that there is a circle with a radius of at least $ 10^{-6} $ which is contained inside all $ n $ circles.

Output three real values, $ x $ , $ y $ , and $ r $ — the coordinates of the center and the radius of the circle.

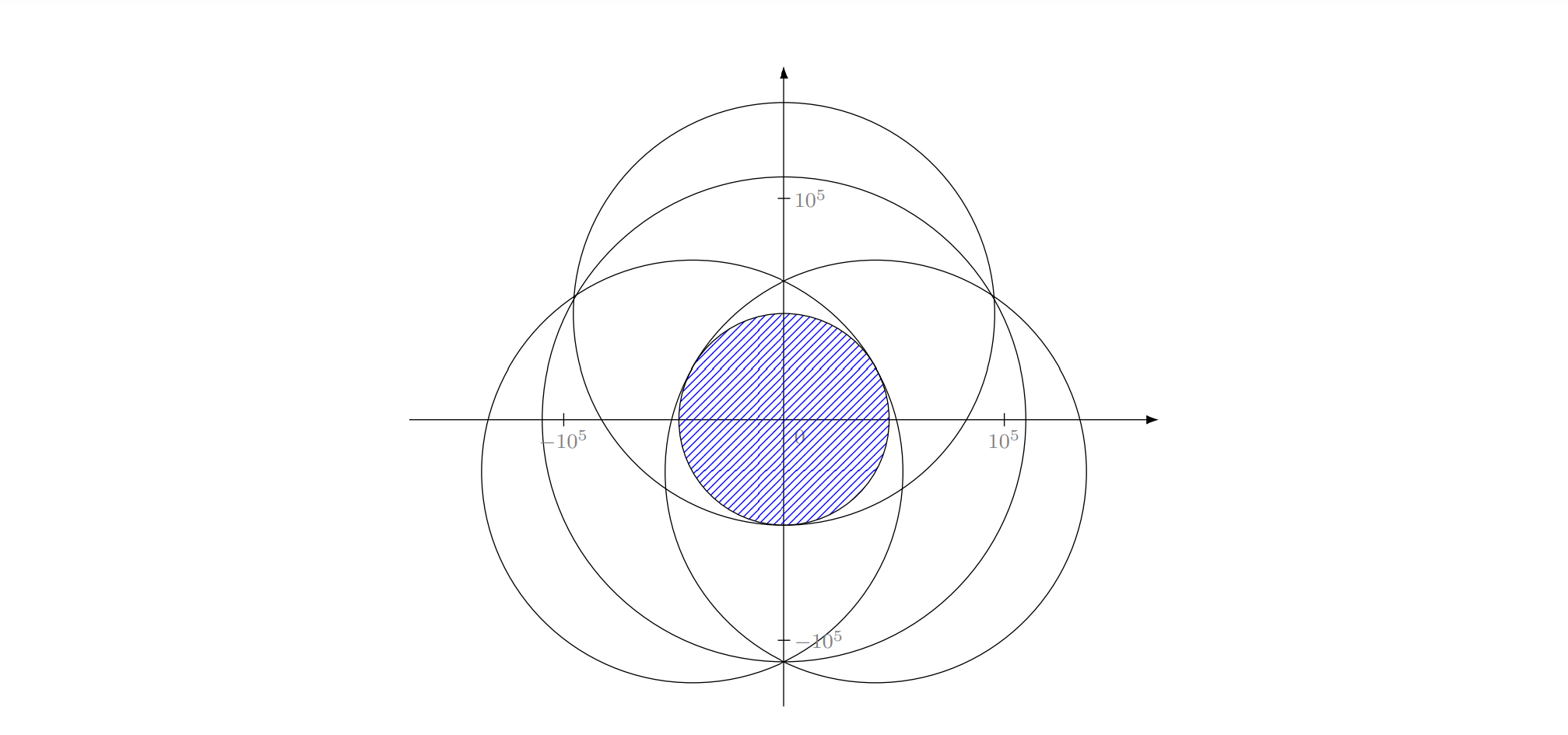
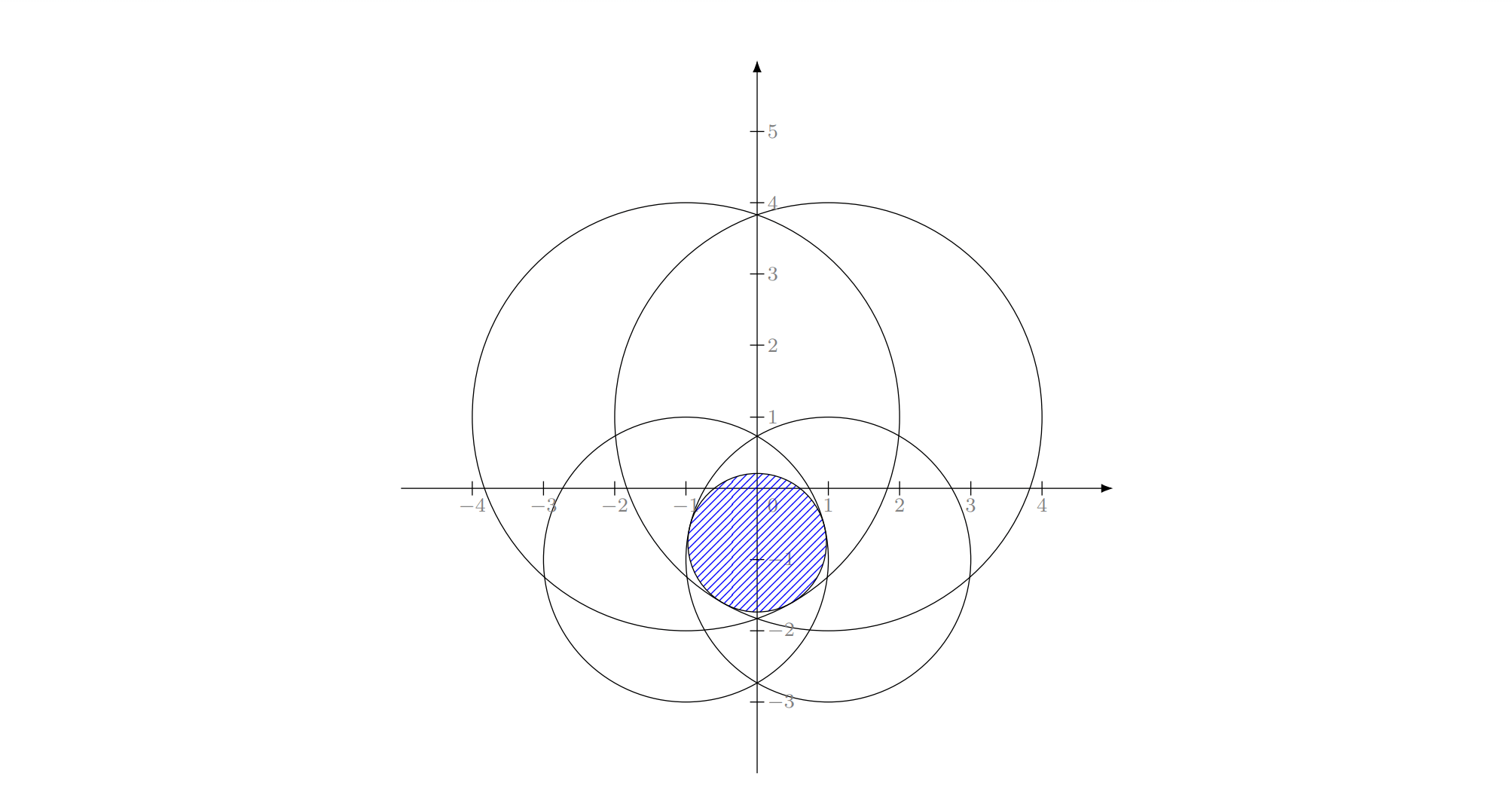A two-dimensional plot depicting the first test case is given below. The output circle $ C $ is dashed with blue lines. A two-dimensional plot depicting the second test case is given below. The output circle $ C $ is dashed with blue lines.