CF193A Cutting Figure

You've gotten an $ n×m $ sheet of squared paper. Some of its squares are painted. Let's mark the set of all painted squares as $ A $ . Set $ A $ is connected. Your task is to find the minimum number of squares that we can delete from set $ A $ to make it not connected. A set of painted squares is called connected, if for every two squares $ a $ and $ b $ from this set there is a sequence of squares from the set, beginning in $ a $ and ending in $ b $ , such that in this sequence any square, except for the last one, shares a common side with the square that follows next in the sequence. An empty set and a set consisting of exactly one square are connected by definition.

The first input line contains two space-separated integers $ n $ and $ m $ ( $ 1

On the first line print the minimum number of squares that need to be deleted to make set $ A $ not connected. If it is impossible, print -1.

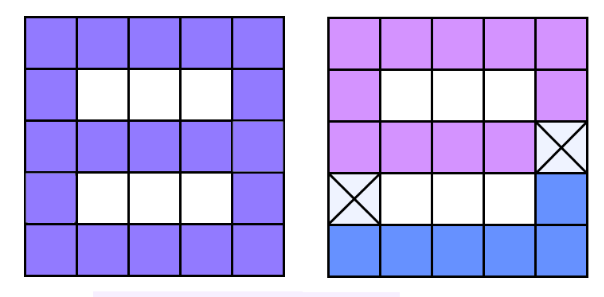
In the first sample you can delete any two squares that do not share a side. After that the set of painted squares is not connected anymore. The note to the second sample is shown on the figure below. To the left there is a picture of the initial set of squares. To the right there is a set with deleted squares. The deleted squares are marked with crosses.