CF193A Cutting Figure

你有一张 $n\times m$ 的方格纸，其中一些格子已经被涂色。我们记所有已涂色格子的集合为 $A$。集合 $A$ 是连通的。你的任务是找出最少需要从集合 $A$ 中删除多少个格子，才能使得 $A$ 不再连通。 一个已涂色格子的集合被称为连通的，如果对于集合中的任意两个格子 $a$ 和 $b$，总可以找到一个由集合中格子组成的序列，从 $a$ 到 $b$，并且在这个序列中，除了最后一个格子之外，每个格子都与下一个格子有公共边。空集和仅包含一个格子的集合都被定义为连通的。

输入的第一行包含两个用空格分隔的整数 $n$ 和 $m$（$1\leq n,m\leq 50$），表示方格纸的大小。 接下来的 $n$ 行，每行包含 $m$ 个字符，描述整张纸：第 $i$ 行第 $j$ 列上的字符为 “#”，表示对应的格子已经被涂色（属于集合 $A$），为 “.” 表示该格子没有被涂色（不属于集合 $A$）。保证所有已涂色格子形成的集合 $A$ 是连通且非空。

输出一行，表示要使集合 $A$ 不连通，最少需要删除多少个格子。如果无法做到，输出 $-1$。

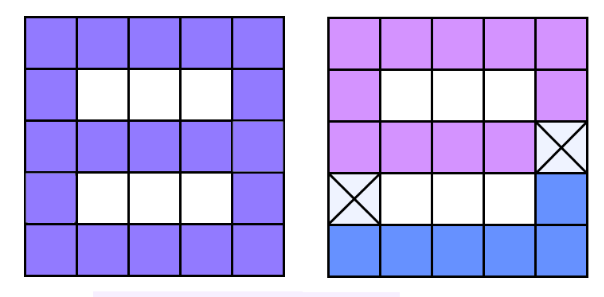
在第一个样例中，可以删除任意两个不相邻的格子。删除后，集合 $A$ 将不再连通。 第二个样例的说明见下图，左侧是初始状态，右侧是删除格子后的状态，被删除的格子用叉号标记。  由 ChatGPT 5 翻译