CF1942C2 Bessie's Birthday Cake (Hard Version)

[Proof Geometric Construction Can Solve All Love Affairs - manbo-p](https://soundcloud.com/alice-law-314125270/manbo-p-proof-geometric-construction-can-solve-all-love-affairs) ⠀ 这是该问题的困难版本。两个版本的唯一区别在于 $y$ 的限制。在本版本中，$0 \leq y \leq n - x$。只有当两个版本都被解决时，你才能进行 hack。 Bessie 收到了她最好的朋友 Elsie 送来的生日蛋糕，这个蛋糕是一个正 $n$ 边形。蛋糕的顶点从 $1$ 到 $n$ 顺时针编号。你和 Bessie 将从这些顶点中选择一些，来在蛋糕上切出不相交的对角线。换句话说，对角线的两个端点必须是被选中的顶点。 Bessie 只想分发那些能形成三角形的蛋糕块，以保持一致性。蛋糕块的大小无关紧要，整个蛋糕不必全部被分成三角形（蛋糕中可以有其他形状，但这些不会被计数）。 Bessie 已经选好了 $x$ 个可以用来画对角线的顶点。她希望你再选择不超过 $y$ 个其他顶点，使得她能分发的三角形蛋糕块的数量最大。 Bessie 最多能分发多少个不相交的三角形蛋糕块？

第一行包含一个整数 $t$（$1 \leq t \leq 10^4$），表示测试用例的数量。 每个测试用例的第一行包含三个整数 $n$、$x$ 和 $y$（$4 \leq n \leq 10^9$，$2 \leq x \leq \min(n, 2 \cdot 10^5)$，$0 \leq y \leq n - x$），分别表示多边形的边数、Bessie 已选的顶点数以及你最多可以再选的顶点数。 第二行包含 $x$ 个互不相同的整数，范围为 $1$ 到 $n$，表示 Bessie 已经选中的顶点。 保证所有测试用例中 $x$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，输出一个整数，表示 Bessie 最多能分发多少个不相交的三角形蛋糕块。

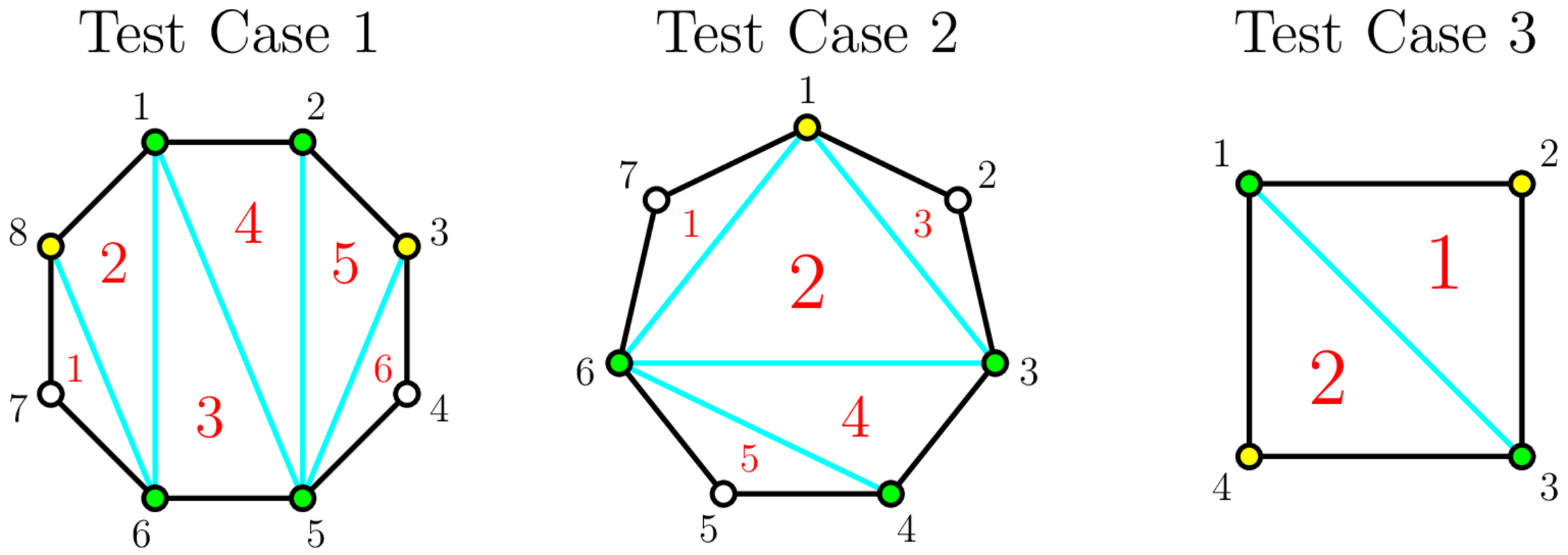
在第 $1$、$2$ 和 $3$ 个测试用例中，你可以分别获得 $6$、$5$ 和 $2$ 个不相交的三角形蛋糕块。如下图所示为一种可能的构造方式： 绿色点表示 Bessie 选中的顶点，黄色点表示你选中的顶点，蓝色线表示画出的对角线，红色数字表示被计数的三角形。  由 ChatGPT 4.1 翻译