CF1942D Learning to Paint

[Pristine Beat - Touhou](https://soundcloud.com/jackaltroy/sets/primordial-beat-pristine-beat) ⠀ Elsie is learning how to paint. She has a canvas of $ n $ cells numbered from $ 1 $ to $ n $ and can paint any (potentially empty) subset of cells. Elsie has a 2D array $ a $ which she will use to evaluate paintings. Let the maximal contiguous intervals of painted cells in a painting be $ [l_1,r_1],[l_2,r_2],\ldots,[l_x,r_x] $ . The beauty of the painting is the sum of $ a_{l_i,r_i} $ over all $ 1 \le i \le x $ . In the image above, the maximal contiguous intervals of painted cells are $ [2,4],[6,6],[8,9] $ and the beauty of the painting is $ a_{2,4}+a_{6,6}+a_{8,9} $ . There are $ 2^n $ ways to paint the strip. Help Elsie find the $ k $ largest possible values of the beauty of a painting she can obtain, among all these ways. Note that these $ k $ values do not necessarily have to be distinct. It is guaranteed that there are at least $ k $ different ways to paint the canvas.

The first line contains a single integer $ t $ ( $ 1 \leq t \leq 10^3 $ ) — the number of test cases. The first line of each test case contains $ 2 $ integers $ n $ and $ k $ ( $ 1 \leq n \leq 10^3 $ , $ 1 \leq k \leq \min(2^n, 5 \cdot 10^3) $ ) — the number of cells and the number of largest values of the beauty of a painting you must find. The next $ n $ lines of each test case describe $ a $ where the $ i $ -th of which contains $ n-i+1 $ integers $ a_{i,i},a_{i,i+1},\ldots,a_{i,n} $ ( $ -10^6 \leq a_{i,j} \leq 10^6 $ ). It is guaranteed the sum of $ n $ over all test cases does not exceed $ 10^3 $ and the sum of $ k $ over all test cases does not exceed $ 5 \cdot 10^3 $ .

For each test case, output $ k $ integers in one line: the $ i $ -th of them must represent the $ i $ -th largest value of the beauty of a painting Elsie can obtain.

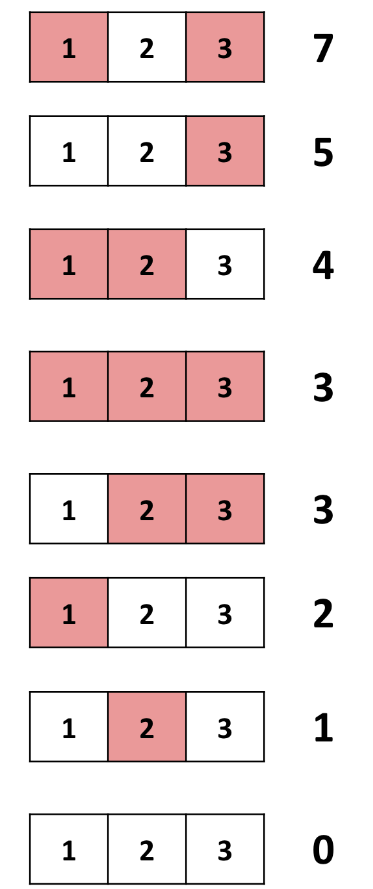
In the first test case, Elsie can either paint the only cell or not paint it. If she paints the only cell, the beauty of the painting is $ -5 $ . If she chooses not to paint it, the beauty of the painting is $ 0 $ . Thus, the largest beauty she can obtain is $ 0 $ and the second largest beauty she can obtain is $ -5 $ . Below is an illustration of the third test case.