CF1949A Grove
题目描述
你想在一个边长为 $ n $ 的正方形草坪上种树。这个草坪的四个角在笛卡尔坐标系下的坐标分别是 $ (0, 0) $、$ (n, 0) $、$ (0, n) $ 和 $ (n, n) $。树只能种在整数坐标的位置上。每棵树的根系会向周围扩展,覆盖一个以该位置为中心、半径为 $ r $ 的圆形区域。这个圆形区域必须完全位于草坪内部(可以接触草坪的边界),此外,圆形区域之间只能在边缘接触,不能重叠。
你的任务是寻找一种排列方式,使得能种最多的树。
输入格式
输入包含一行,给出一个整数 $ n $($ 1 \leq n \leq 20 $)和一个实数 $ r $($ 0 < r \leq n/2 $)。这两个数分别表示草坪的边长和每棵树根系生长的圆盘半径。半径 $ r $ 以小数形式给出,小数点后的位数至少 1 位,最多 3 位。
输出格式
第一行输出可以种植的最大树木数量 $ m $。
接下来的 $ m $ 行,每行两个整数 $ x $ 和 $ y $,表示第 $ i $ 棵树种植的位置的坐标。树可以按任意顺序输出。
若有多种方案,输出其中任意一种即可。
说明/提示
以下例子展示了一种种植方案。注意,这并不是唯一能达到最大化种植数量的方法。
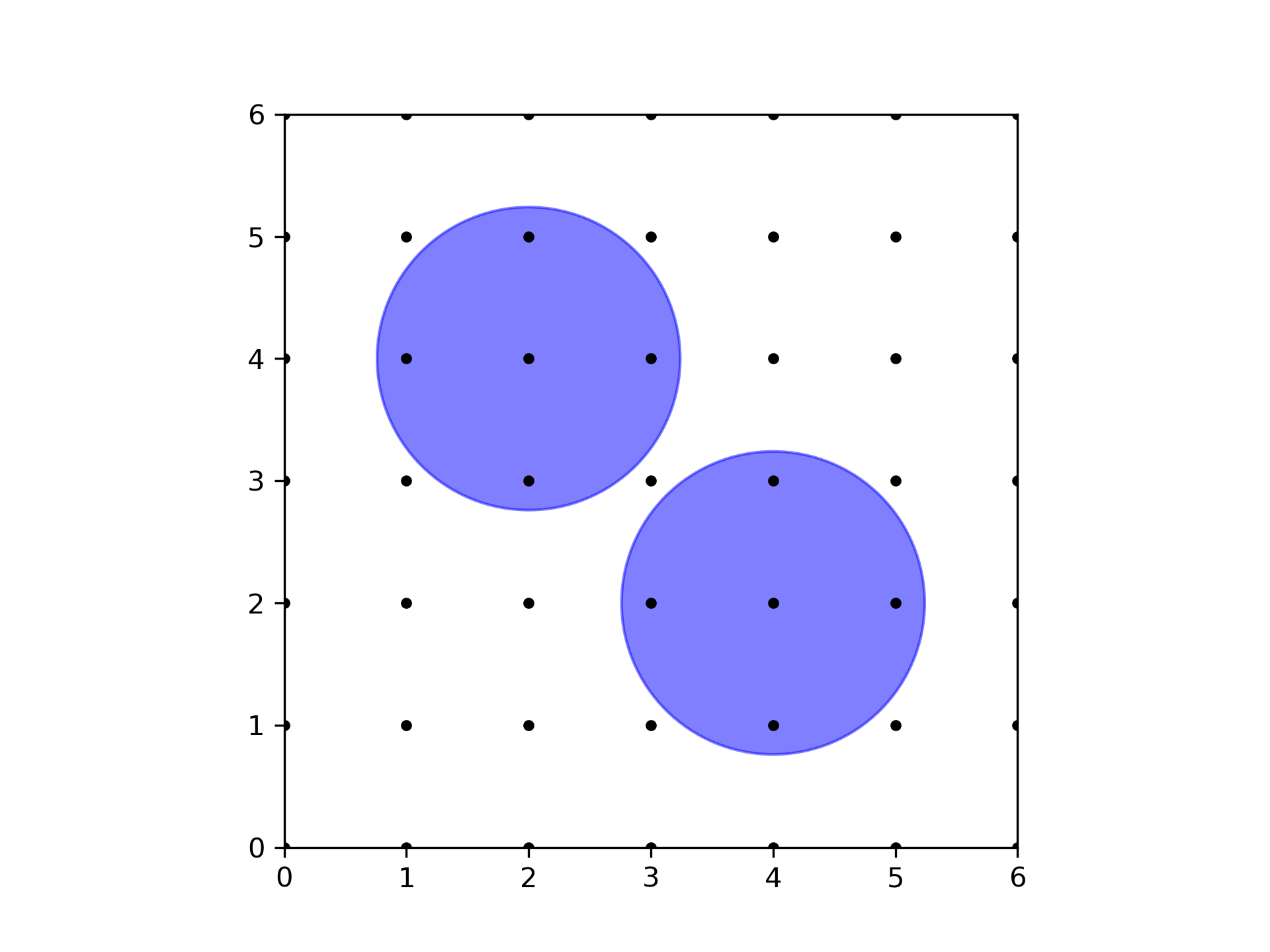
另一个例子展示的方案也是如此。
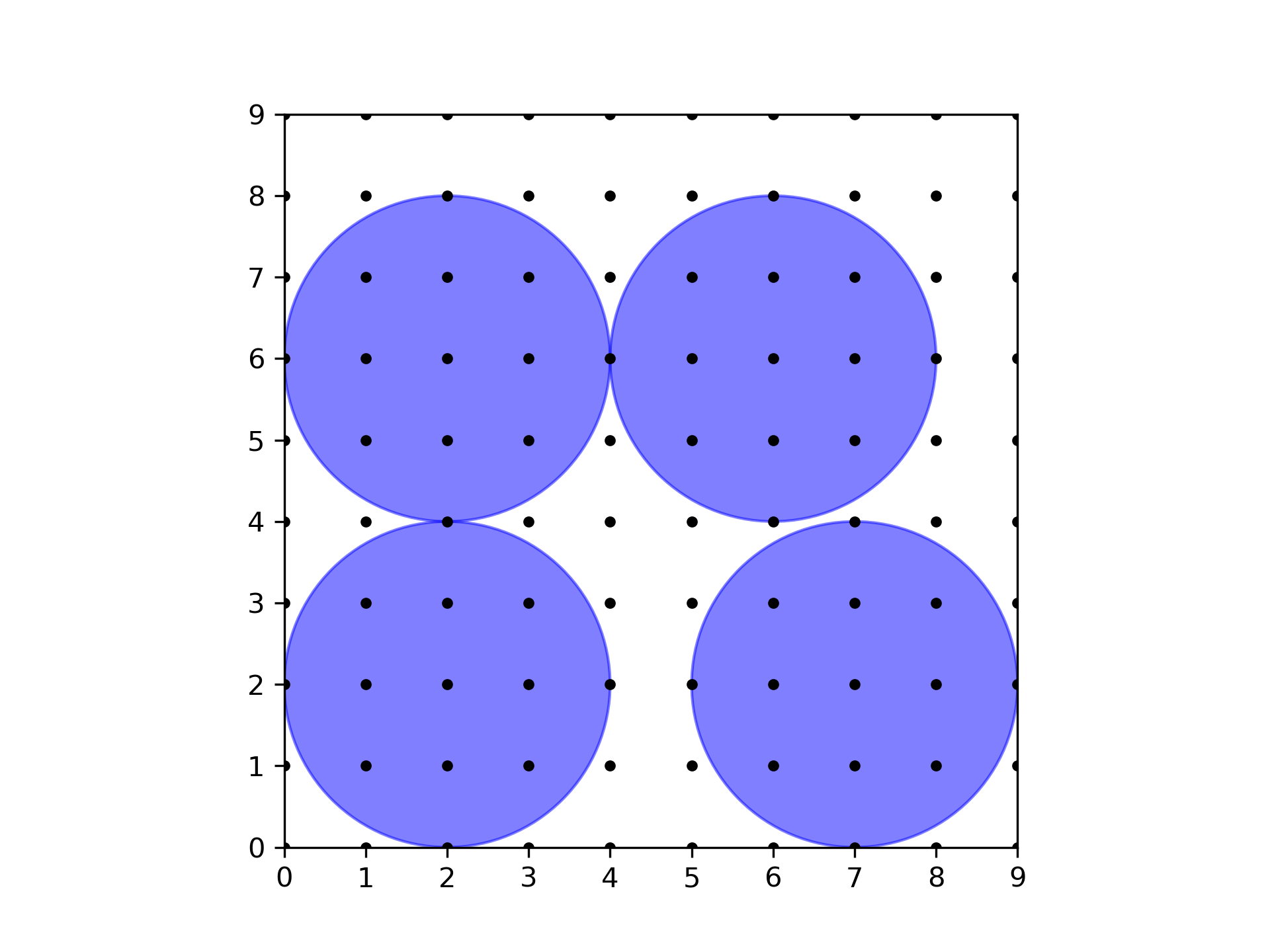
**本翻译由 AI 自动生成**