CF1949A Grove

You want to plant trees in a square lawn of size $ n \times n $ whose corners have Cartesian coordinates $ (0, 0) $ , $ (n, 0) $ , $ (0, n) $ , and $ (n, n) $ . Trees can only be planted at locations with integer coordinates. Every tree will grow roots within a disk of radius $ r $ centered at the location where the tree was planted; such disks must be fully contained in the lawn (possibly touching the boundary of the lawn) and can only intersect each other on their boundaries. Find a configuration that maximizes the number of trees.

The first and only line contains an integer $ n $ ( $ 1 \leq n \leq 20 $ ) and a real number $ r $ ( $ 0 < r \leq n/2 $ ) — the length of the sides of the lawn, and the radius of the disks where each tree will grow roots. The real number $ r $ is given in decimal notation with at least $ 1 $ and at most $ 3 $ digits after the decimal point.

In the first line, print the maximum number $ m $ of trees that can be planted. In the next $ m $ lines, print a configuration that maximizes the number of trees. Specifically, in the $ (i+1) $ -th line, print two integers $ x $ and $ y $ — the coordinates of the location where the $ i $ -th tree should be planted. You can print the trees in any order. If there are multiple solutions, print any of them.

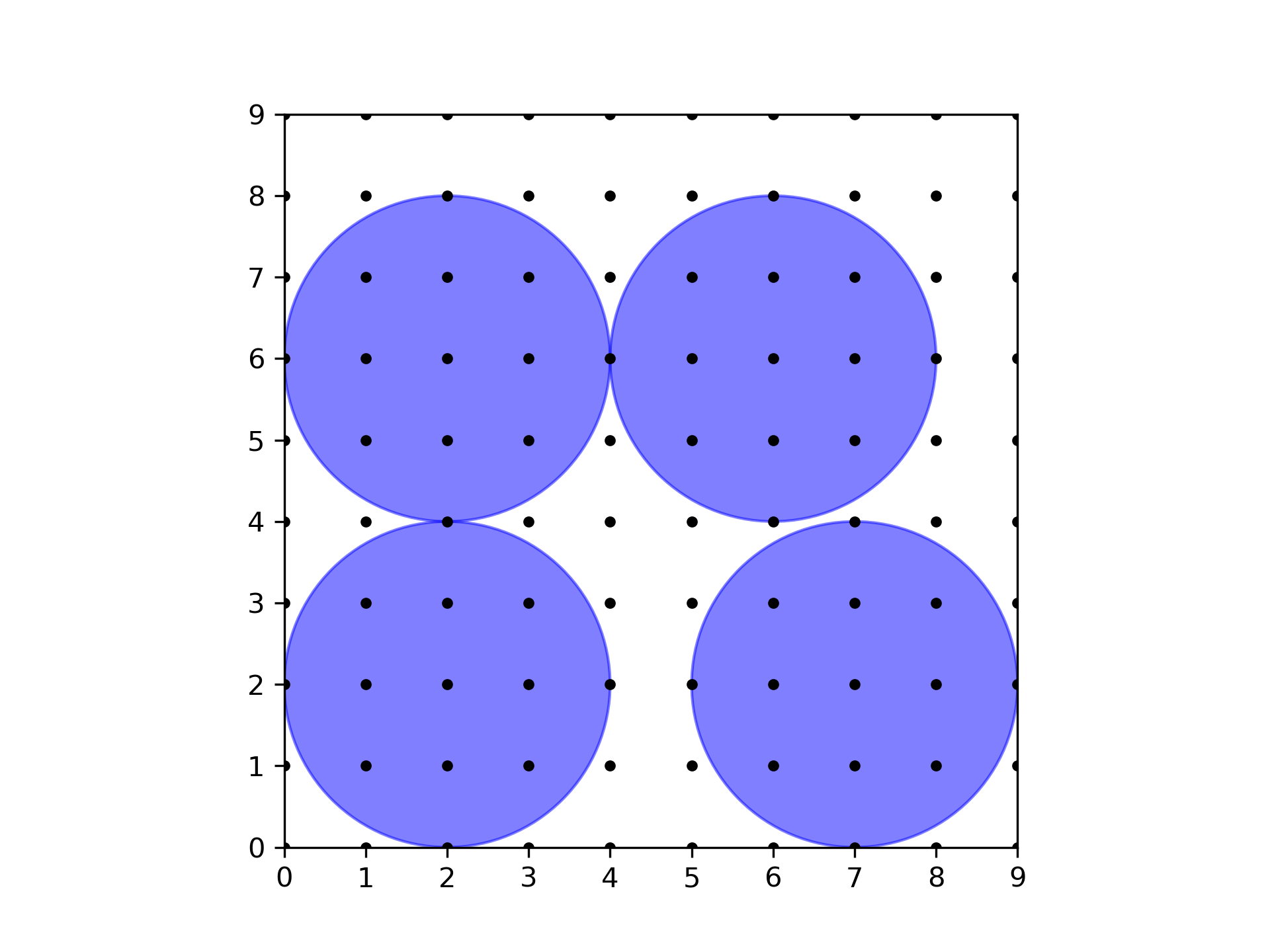
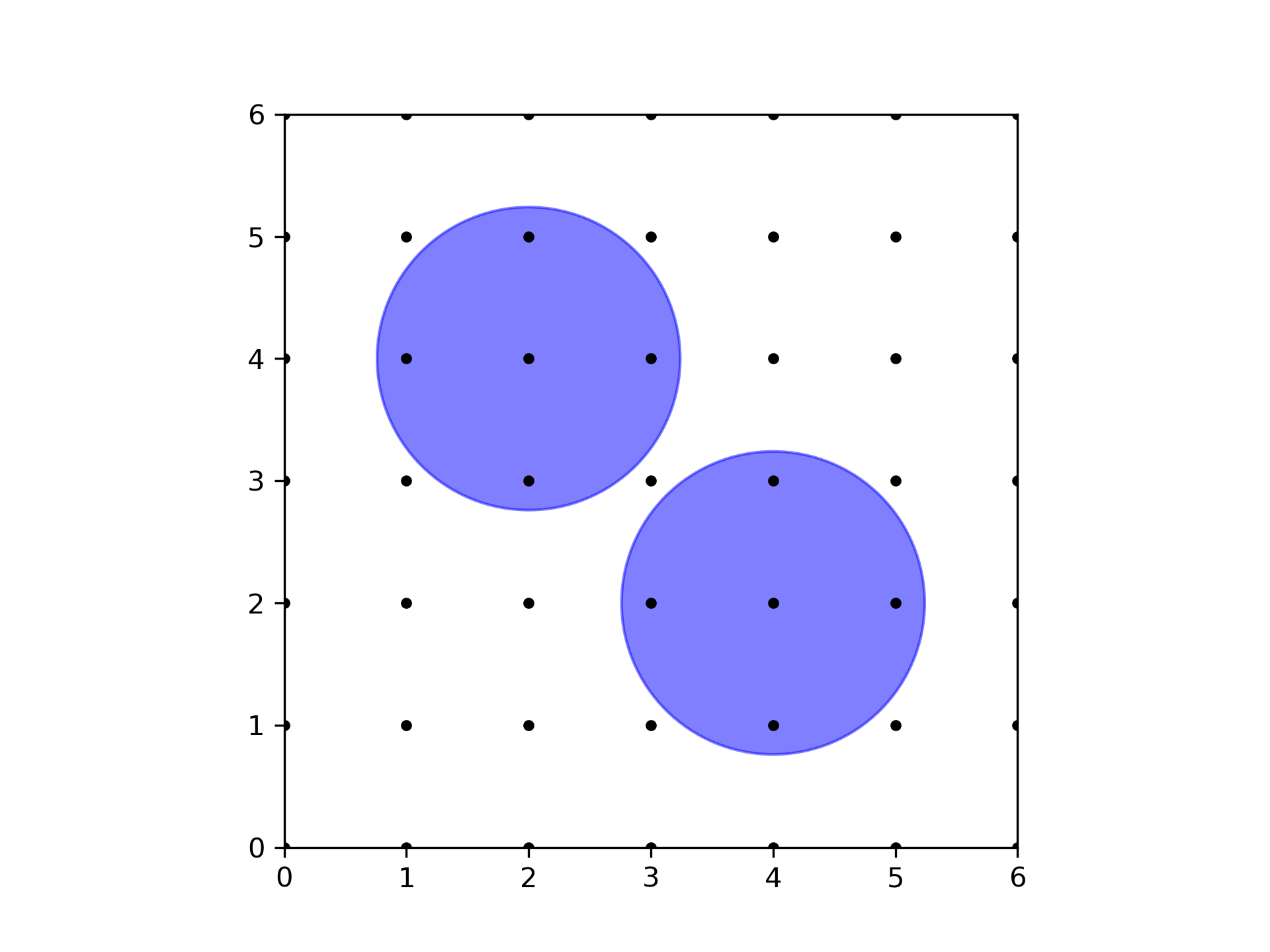For the first sample, the sample output is shown in the following figure. Note that this is not the only configuration that maximizes the number of trees. For the second sample, the sample output is shown in the following figure. Note that this is not the only configuration that maximizes the number of trees.