CF1949I Disks

# 圆盘 你在平面上有 $ n $ 个圆盘。每个圆盘的中心具有整数坐标，每个圆盘的半径为正整数。没有两个圆盘在一个正面积的区域重叠，但圆盘之间可能相切。 你的任务是确定是否可以改变圆盘的半径，使得： - 原来相切的圆盘仍然相切。 - 没有两个圆盘在一个正面积的区域重叠。 - 所有半径的总和严格减小。 新的半径可以是任意正实数。不能改变圆盘的中心。

第一行包含一个整数 $ n $ （ $ 1\le n \le 1000 $ ）— 圆盘的数量。 接下来的 $ n $ 行，每行包含三个整数。第 $ i $ 行包含 $ x_i $ ， $ y_i $ （ $ -10^9 \leq x_i, y_i \le 10^9 $ ），以及 $ r_i $ （ $ 1 \leq r_i \le 10^9 $ ）— 第 $ i $ 个圆盘的中心坐标和半径。

如果可以按照要求改变半径，则打印 $ \texttt{YES} $ 。否则，打印 $ \texttt{NO} $ 。 ## 样例 #1 ### 样例输入 #1 ``` 5 0 2 1 0 0 1 4 -3 4 11 0 3 11 5 2 ``` ### 样例输出 #1 ``` YES ``` ## 样例 #2 ### 样例输入 #2 ``` 4 2 2 2 7 2 3 7 7 2 2 7 3 ``` ### 样例输出 #2 ``` NO ```

在第一个样例中，可以将第一个和第三个圆盘的半径减小 $ 0.5 $ ，将第二个圆盘的半径增加 $ 0.5 $ 。这样，所有半径的总和减小了 $ 0.5 $ 。改变半径前后的情况如下图所示。 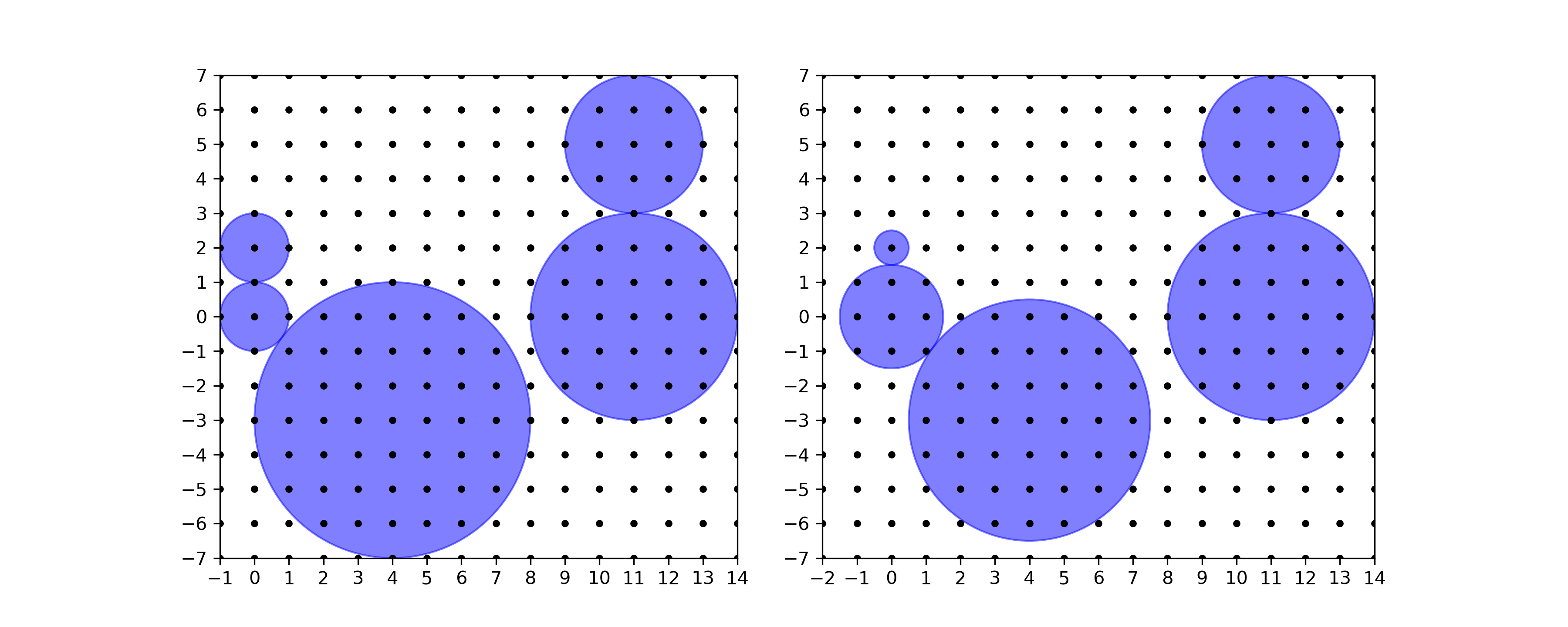 第一个样例（左）和改变圆盘半径的有效方法（右）。在第二个样例中，如下图所示，无法按照要求改变圆盘的半径。 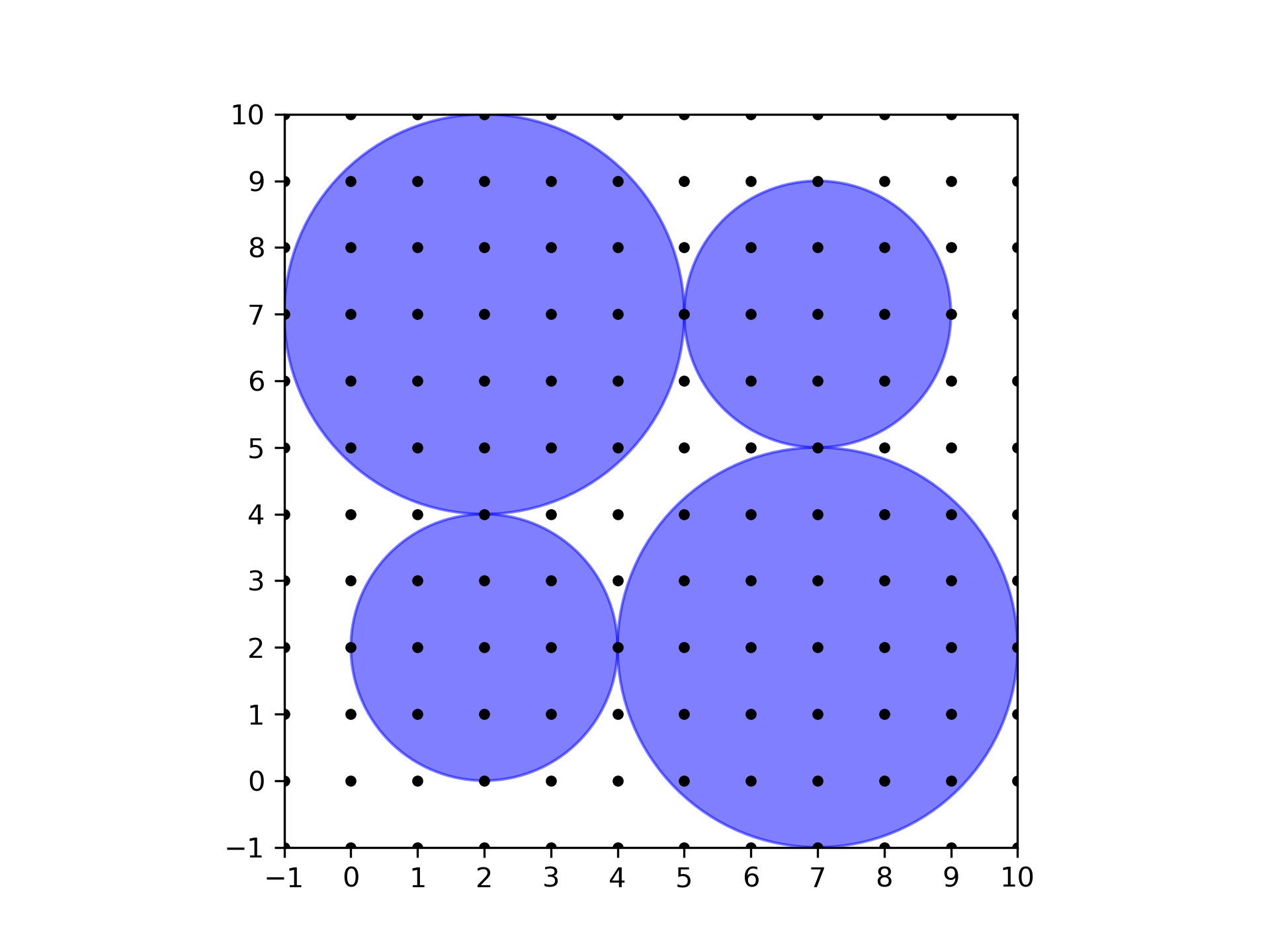 第二个样例。