CF1949J Amanda the Amoeba
题目描述
如图,$r\times c$ 的网格中有一只变形虫。每个格子有三种状态:被变形虫的身体占据(绿色),空白(白色),或存在障碍物(黑色)。
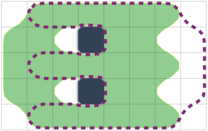
每次移动,先将身体占据的格子之一变为空白,然后再把某个与身体相邻的空白格子变为身体所占据。两个格子相邻当且仅当有公共边。移动过程中要保证身体是连通的,且不占据障碍物。
已知变形虫初始占据了哪些格子,它想移动到占据着给出的另一些格子(虚线内)的状态。求任意一种方案。
输入格式
第一行 $r, c.$
下面的 $r$ 行 $c$ 列,表示初始状态;接下去又有 $r$ 行 $c$ 列,表示目标状态。其中,`*` 表示变形虫的身体,`.` 表示空白,`X` 表示障碍。
$r, c\leq 50$
输出格式
若不存在方案,输出 `NO`;否则先输出一行 `YES`,然后一行一个整数 $m$ 表示移动次数。
接下来 $m$ 行,每行 $4$ 个整数 $x_1, y_1, x_2, y_2$ 表示该次移动时,变空白的格子、新占据的格子。
可以证明只要有方案,就存在 $m\leq 10^4$ 的方案。
说明/提示
In the first sample, Amanda executes 5 moves to reach the final position, as shown in the figure below.
