CF1950F 0, 1, 2, Tree!
题目描述
查找满足条件的有根树 $^{\dagger}$ 的最小高度。
其中 $a+b+c$ 个顶点满足以下条件:
- $a$ 个顶点恰好有 $2$ 个子顶点,
- $b$ 个顶点恰好有 $1$ 个子顶点,
- $c$ 个顶点没有子顶点。
如果没有这样的树,输出 $-1$。
如:
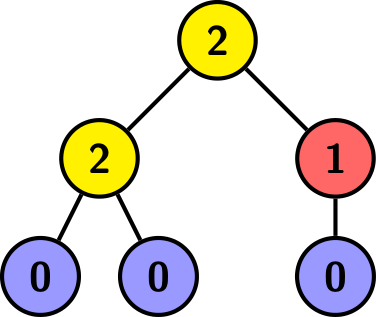
上面的树植根于顶部顶点,每个顶点都标有它的子节点数。
这里 $a=2,b=1,c=3$,高度为 $2$。
$^{\dagger}$:有根树是指一个没有循环的连通图,有一个特殊的顶点称为根。在有根树中,在由边连接的任意两个顶点,一个顶点是父顶点(离根更近的顶点),另一个是子顶点。
树中两个顶点之间的距离是它们之间最短路径中的边数。有根树的高度是从顶点到根部的最大距离。
输入格式
第一行包含一个整数 $t$($1\leq t\leq 10^4$)表示测试用例的数量。
每个测试用例的唯一一行包含三个整数 $a$,$b$ 和 $c$($0\leq a、b、c\leq 10^5$;$1\leq a+b+c$)。
所有测试用例的 $a+b+c$ 之和不超过 $3 \cdot 10^5$。
输出格式
对于每个测试用例,如果不存在这样的树,输出 $-1$。
否则输出一个整数——满足条件的树的最小高度。
## 样例 #1
### 样例输入 #1
```
10
2 1 3
0 0 1
0 1 1
1 0 2
1 1 3
3 1 4
8 17 9
24 36 48
1 0 0
0 3 1
```
### 样例输出 #1
```
2
0
1
1
-1
3
6
-1
-1
3
```
说明/提示
第一个测试用例如图所示。树的高度不能低于 $2$。
在第二个测试用例中,您可以形成一个只有一个顶点且没有边的树。它的高度为 $0$,这显然是最佳的。
在第三个测试用例中,您可以形成一个由单个边连接的两个顶点的树。它的高度为 $1$,这显然是最佳的。