CF1950F 0, 1, 2, Tree!

Find the minimum height of a rooted tree $ ^{\dagger} $ with $ a+b+c $ vertices that satisfies the following conditions: - $ a $ vertices have exactly $ 2 $ children, - $ b $ vertices have exactly $ 1 $ child, and - $ c $ vertices have exactly $ 0 $ children. If no such tree exists, you should report it. 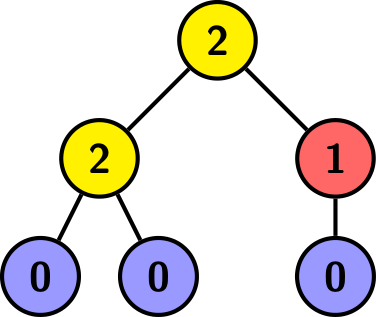The tree above is rooted at the top vertex, and each vertex is labeled with the number of children it has. Here $ a=2 $ , $ b=1 $ , $ c=3 $ , and the height is $ 2 $ . $ ^{\dagger} $ A rooted tree is a connected graph without cycles, with a special vertex called the root. In a rooted tree, among any two vertices connected by an edge, one vertex is a parent (the one closer to the root), and the other one is a child. The distance between two vertices in a tree is the number of edges in the shortest path between them. The height of a rooted tree is the maximum distance from a vertex to the root.

The first line contains an integer $ t $ ( $ 1 \leq t \leq 10^4 $ ) — the number of test cases. The only line of each test case contains three integers $ a $ , $ b $ , and $ c $ ( $ 0 \leq a, b, c \leq 10^5 $ ; $ 1 \leq a + b + c $ ). The sum of $ a + b + c $ over all test cases does not exceed $ 3 \cdot 10^5 $ .

For each test case, if no such tree exists, output $ -1 $ . Otherwise, output one integer — the minimum height of a tree satisfying the conditions in the statement.

The first test case is pictured in the statement. It can be proven that you can't get a height smaller than $ 2 $ . In the second test case, you can form a tree with a single vertex and no edges. It has height $ 0 $ , which is clearly optimal. In the third test case, you can form a tree with two vertices joined by a single edge. It has height $ 1 $ , which is clearly optimal.