CF1951I Growing Trees

[wowaka ft. 初音未来 - Ura-Omote Lovers](https://youtu.be/b_cuMcDWwsI) ඞ 给定一个无向连通简单图，包含 $n$ 个节点和 $m$ 条边，第 $i$ 条边连接节点 $u_i$ 和 $v_i$，并带有两个正参数 $a_i$ 和 $b_i$。此外，还给定一个整数 $k$。 如果一个大小为 $m$ 的非负数组 $x$ 满足以下条件，则称其为 $k$-生成树生成器： - 考虑一个有 $n$ 个节点的无向多重图，其中第 $i$ 条边被克隆了 $x_i$ 次（即有 $x_i$ 条边连接 $u_i$ 和 $v_i$）。可以将该图的所有边划分为 $k$ 棵生成树，每条边恰好属于一棵生成树$^\dagger$。 该数组 $x$ 的代价定义为 $\sum_{i = 1}^m a_i x_i^2 + b_i x_i$。请你求出 $k$-生成树生成器的最小代价。 $^\dagger$ 多重图的生成树是指该图的一组边，能够连通所有顶点且不形成环。

每个测试包含多组数据。第一行包含一个整数 $t$（$1 \le t \le 500$）——测试用例的数量。每组测试数据描述如下。 每组测试数据的第一行包含三个整数 $n$、$m$ 和 $k$（$2 \le n \le 50, n - 1 \le m \le \min(50, \frac{n(n - 1)}{2}), 1 \le k \le 10^7$）——图的节点数、边数和 $k$-生成树生成器的参数。 接下来的 $m$ 行，每行包含四个整数 $u_i$、$v_i$、$a_i$ 和 $b_i$（$1 \le u_i, v_i \le n, u_i \neq v_i, 1 \le a_i, b_i \le 1000$）——第 $i$ 条边的两个端点及其参数。保证图是简单且连通的。 保证所有测试用例中 $n^2$ 的和与 $m^2$ 的和均不超过 $2500$。

对于每组测试数据，输出一个整数：$k$-生成树生成器的最小代价。

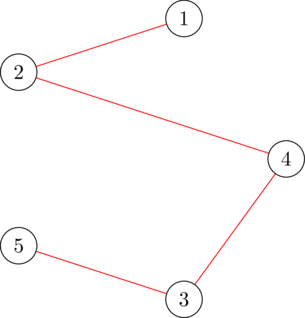
在第一个测试用例中，一个合法的 $1$-生成树生成器为 $x = [1, 1, 1, 1, 0]$，如下图所示。该生成器的代价为 $(1^2 \cdot 5 + 1 \cdot 5) + (1^2 \cdot 5 + 1 \cdot 7) + (1^2 \cdot 6 + 1 \cdot 2) + (1^2 \cdot 3 + 1 \cdot 5) + (0^2 \cdot 4 + 0 \cdot 9) = 38$。可以证明不存在更低代价的生成器。  $x = [1, 1, 1, 1, 0]$ 的 $1$-生成树划分 在第二个测试用例中，一个合法的 $3$-生成树生成器为 $x = [2, 3, 2, 2, 3]$，如图所示。该生成器的代价为 $(2^2 \cdot 5 + 2 \cdot 5) + (3^2 \cdot 5 + 3 \cdot 7) + (2^2 \cdot 6 + 2 \cdot 2) + (2^2 \cdot 3 + 2 \cdot 5) + (3^2 \cdot 4 + 3 \cdot 9) = 191$。可以证明不存在更低代价的生成器。  $x = [2, 3, 2, 2, 3]$ 的 $3$-生成树划分 由 ChatGPT 4.1 翻译