CF1951I Growing Trees

[wowaka ft. Hatsune Miku - Ura-Omote Lovers](https://youtu.be/b_cuMcDWwsI) ඞ You are given an undirected connected simple graph with $ n $ nodes and $ m $ edges, where edge $ i $ connects node $ u_i $ and $ v_i $ , with two positive parameters $ a_i $ and $ b_i $ attached to it. Additionally, you are also given an integer $ k $ . A non-negative array $ x $ with size $ m $ is called a $ k $ -spanning-tree generator if it satisfies the following: - Consider the undirected multigraph with $ n $ nodes where edge $ i $ is cloned $ x_i $ times (i.e. there are $ x_i $ edges connecting $ u_i $ and $ v_i $ ). It is possible to partition the edges of this graph into $ k $ spanning trees, where each edge belongs to exactly one spanning tree $ ^\dagger $ . The cost of such array $ x $ is defined as $ \sum_{i = 1}^m a_i x_i^2 + b_i x_i $ . Find the minimum cost of a $ k $ -spanning-tree generator. $ ^\dagger $ A spanning tree of a (multi)graph is a subset of the graph's edges that form a tree connecting all vertices of the graph.

Each test contains multiple test cases. The first line contains an integer $ t $ ( $ 1 \le t \le 500 $ ) — the number of test cases. The description of the test cases follows. The first line of each test case contains three integers $ n $ , $ m $ , and $ k $ ( $ 2 \le n \le 50, n - 1 \le m \le \min(50, \frac{n(n - 1)}{2}), 1 \le k \le 10^7 $ ) — the number of nodes in the graph, the number of edges in the graph, and the parameter for the $ k $ -spanning-tree generator. Each of the next $ m $ lines of each test case contains four integers $ u_i $ , $ v_i $ , $ a_i $ , and $ b_i $ ( $ 1 \le u_i, v_i \le n, u_i \neq v_i, 1 \le a_i, b_i \le 1000 $ ) — the endpoints of the edge $ i $ and its two parameters. It is guaranteed that the graph is simple and connected. It is guaranteed that the sum of $ n^2 $ and the sum of $ m^2 $ over all test cases does not exceed $ 2500 $ .

For each test case, output a single integer: the minimum cost of a $ k $ -spanning-tree generator.

In the first test case, a valid $ 1 $ -spanning-tree generator is $ x = [1, 1, 1, 1, 0] $ , as indicated by the following figure. The cost of this generator is $ (1^2 \cdot 5 + 1 \cdot 5) + (1^2 \cdot 5 + 1 \cdot 7) + (1^2 \cdot 6 + 1 \cdot 2) + (1^2 \cdot 3 + 1 \cdot 5) + (0^2 \cdot 4 + 0 \cdot 9) = 38 $ . It can be proven that no other generator has a lower cost. 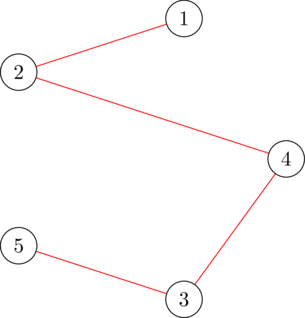 The $ 1 $ -spanning-tree partition of $ x = [1, 1, 1, 1, 0] $ In the second test case, a valid $ 3 $ -spanning-tree generator is $ x = [2, 3, 2, 2, 3] $ , as indicated by the following figure. The cost of this generator is $ (2^2 \cdot 5 + 2 \cdot 5) + (3^2 \cdot 5 + 3 \cdot 7) + (2^2 \cdot 6 + 2 \cdot 2) + (2^2 \cdot 3 + 2 \cdot 5) + (3^2 \cdot 4 + 3 \cdot 9) = 191 $ . It can be proven that no other generator has a lower cost.  The $ 3 $ -spanning-tree partition of $ x = [2, 3, 2, 2, 3] $