CF195D Analyzing Polyline

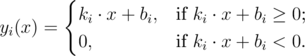
当 Valeric 和 Valerko 在一家体育酒吧观看一场欧洲杯比赛时，他们打碎了一个酒杯。当然，两人支付了赔偿，但酒吧老板说，只有在他们帮助他的儿子完成一个编程任务后才能继续看球。任务如下： 我们考虑如下形式的一组函数：  我们将 $n$ 个给定类型的函数 $y_1(x),\ldots,y_n(x)$ 的和定义为 $s(x) = y_1(x) + \ldots + y_n(x)$。很容易证明，$s(x)$ 的图像是一条折线。你将给出 $n$ 个该类型的函数，你的任务是求出在 $s(x)$ 的图像（也就是所有给定函数的和所得的折线）中，不等于 $180$ 度的角的个数。 Valeric 和 Valerko 真的很想继续看欧洲杯，所以他们请求你帮他们完成。

第一行包含一个整数 $n$，满足 $1 \leq n \leq 10^{5}$，表示函数的数量。 接下来的 $n$ 行中，每行包含两个用空格分隔的整数 $k_i, b_i$，满足 $-10^{9} \leq k_i, b_i \leq 10^{9}$，表示第 $i$ 个函数。

输出一个整数，表示所求折线上所有不等于 $180$ 度的角的数量。

由 ChatGPT 5 翻译