CF1965E Connected Cubes

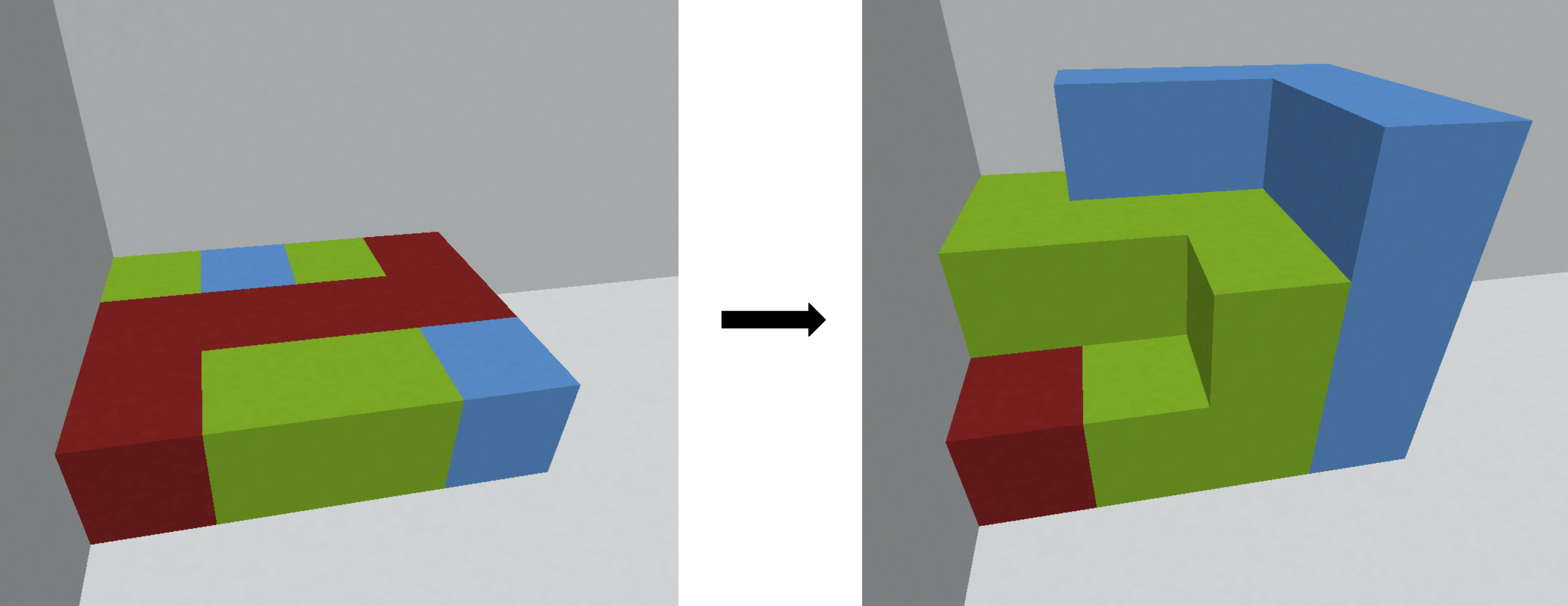
现在有 $n \cdot m$ 个单位立方体，分别位于 $(1, 1, 1)$ 到 $(n, m, 1)$ 的位置。每个立方体都有 $k$ 种颜色中的一种。你可以在任意整数坐标处添加额外的立方体，使得每种颜色的立方体集合都是连通的，其中两个立方体如果有一个面相邻，则认为它们是连通的。 换句话说，对于每一对颜色为 $c$ 的立方体，应当可以只经过颜色为 $c$ 并且两两有公共面的立方体，从一个走到另一个。 现有的立方体位于房间的角落。$x=0$、$y=0$ 和 $z=0$ 的平面上完全被无色立方体填满，不能在这些位置或任何负坐标处放置额外的立方体。  请给出一种方案，使用不超过 $4 \cdot 10^5$ 个额外立方体（不包括当前已有的立方体），或者判断无解。已知在给定约束下，如果有解，则一定存在一种方案，所需额外立方体数量不超过 $4 \cdot 10^5$。

输入的第一行包含三个整数 $n$、$m$ 和 $k$（$2 \le n, m, k \le 50$），分别表示立方体的行数、列数和颜色数。 接下来的 $n$ 行，每行包含 $m$ 个整数。第 $i$ 行第 $j$ 个数为 $a_{ij}$（$1 \le a_{ij} \le k$），表示位置 $(i, j, 1)$ 处立方体的颜色。保证每种颜色 $1$ 到 $k$ 至少出现一次。

如果无解，输出一个整数 $-1$。 否则，输出第一行为一个整数 $p$（$0 \le p \le 4 \cdot 10^5$），表示你添加的额外立方体数量。 接下来的 $p$ 行，每行四个整数 $x$、$y$、$z$ 和 $c$（$1 \le x, y, z \le 10^6$，$1 \le c \le k$），表示在 $(x, y, z)$ 位置添加一个颜色为 $c$ 的立方体。 输出中不应有两个立方体坐标相同，也不能与输入中已有立方体的坐标重复。 如果有多种方案，输出任意一种。

题目描述中的图片对应第一个样例，其中 $\text{red} = 1$，$\text{blue} = 2$，$\text{green} = 3$。 由 ChatGPT 4.1 翻译