CF1968E Cells Arrangement
题目描述
给定一个整数 $n$。你需要在 $n \times n$ 的网格中选择 $n$ 个格子 $(x_1,y_1), (x_2,y_2),\dots,(x_n,y_n)$,其中 $1\le x_i\le n$ 且 $1\le y_i\le n$。
令 $\mathcal{H}$ 为任意两格之间的不同曼哈顿距离的集合。你的任务是最大化集合 $\mathcal{H}$ 的大小。相关构造的示例见题目说明。
如果存在多个解,你可以输出任意一个。
两个格子 $(x_1,y_1)$ 和 $(x_2,y_2)$ 之间的曼哈顿距离为 $|x_1-x_2|+|y_1-y_2|$。
输入格式
第一行包含一个整数 $t$($1\le t\le 50$),表示测试用例的数量。
接下来的 $t$ 行,每行包含一个整数 $n$($2\le n\le 10^3$)。
输出格式
对于每个测试用例,输出 $n$ 个点的坐标,使得集合 $\mathcal{H}$ 的大小最大化。每个点一行,格式为 $x\ y$。
每个测试用例的答案之间不需要输出空行。
说明/提示
在第一个测试用例中,$n=2$。一种可能的方案如下:
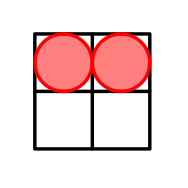
格子位于 $(1,1)$ 和 $(1,2)$。此时 $\mathcal{H}=\{|1-1|+|1-1|,|1-1|+|2-2|,|1-1|+|1-2|\}=\{0,0,1\}=\{0,1\}$。因此,$\mathcal{H}$ 的大小为 $2$。可以证明这是最大可能的答案。
在第二个测试用例中,$n=3$。最优方案如下:
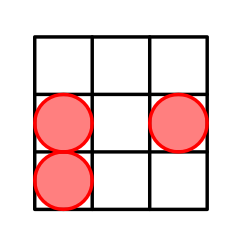
格子位于 $(2,1)$、$(2,3)$ 和 $(3,1)$。$\mathcal{H} = \{|2-2|+|1-1|,|2-2|+|3-3|,|3-3|+|1-1|,|2-2|+|1-3|,|2-3|+|1-1|,|2-3|+|3-1|\} = \{0,0,0,2,1,3\} = \{0,1,2,3\}$。
对于 $n=4$,一种可能的方案如下:
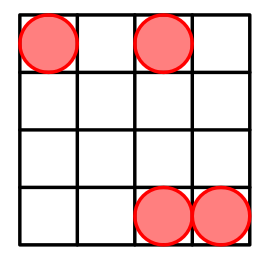
对于 $n=5$,一种可能的方案如下:
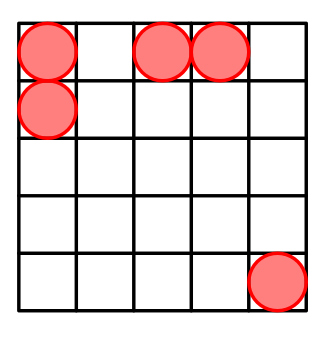
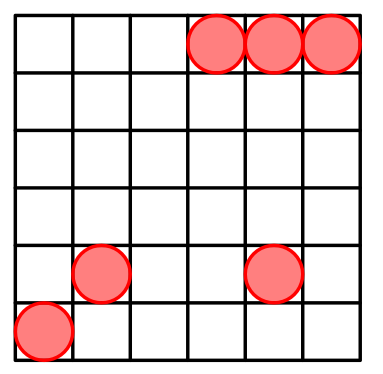
对于 $n=6$,一种可能的方案如下:
由 ChatGPT 4.1 翻译