CF196B Infinite Maze

We've got a rectangular $ n×m $ -cell maze. Each cell is either passable, or is a wall (impassable). A little boy found the maze and cyclically tiled a plane with it so that the plane became an infinite maze. Now on this plane cell $ (x,y) $ is a wall if and only if cell 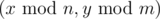 is a wall. In this problem 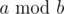 is a remainder of dividing number $ a $ by number $ b $ . The little boy stood at some cell on the plane and he wondered whether he can walk infinitely far away from his starting position. From cell $ (x,y) $ he can go to one of the following cells: $ (x,y-1) $ , $ (x,y+1) $ , $ (x-1,y) $ and $ (x+1,y) $ , provided that the cell he goes to is not a wall.

The first line contains two space-separated integers $ n $ and $ m $ ( $ 1

Print "Yes" (without the quotes), if the little boy can walk infinitely far from the starting point. Otherwise, print "No" (without the quotes).

In the first sample the little boy can go up for infinitely long as there is a "clear path" that goes vertically. He just needs to repeat the following steps infinitely: up, up, left, up, up, right, up. In the second sample the vertical path is blocked. The path to the left doesn't work, too — the next "copy" of the maze traps the boy.