CF1970B2 Exact Neighbours (Medium)

本题与难度更高的版本唯一的区别是 $a_{1} = 0$。 在食死徒最近对霍格沃茨城堡的袭击之后，凤凰社决定在霍格莫德村驻扎 $n$ 名成员。房屋将建在一块风景如画的 $n\times n$ 正方形场地上。每位巫师将拥有属于自己的房屋，每座房屋都归某位巫师所有。每座房屋占据一个格子。 然而，正如你所知，巫师们非常迷信。在周末，每位巫师 $i$ 希望拜访距离自己房屋恰好 $a_{i}$ 格远的另一座房屋（$0 \leq a_{i} \leq n$）。村中的道路仅沿水平方向和垂直方向修建，因此在 $n\times n$ 场地上，点 $(x_{i}, y_{i})$ 与 $(x_{j}, y_{j})$ 之间的距离为 $|x_{i} - x_{j}| + |y_{i} - y_{j}|$。巫师们彼此信任，因此当某位巫师外出时，其他巫师可以拜访他的房屋。房屋足够大，能够容纳所有 $n$ 位巫师同时拜访任意一座房屋。 除此之外，每位巫师都必须拥有面朝北方霍格沃茨城堡和南方禁林的视野，因此任何一位巫师的房屋都不能遮挡其他人的视线。具体来说，在 $n\times n$ 场地的每一列中，最多只能有一座房屋。也就是说，如果第 $i$ 座房屋的坐标为 $(x_{i}, y_{i})$，则对于所有 $i \neq j$，都有 $x_{i} \neq x_{j}$。 凤凰社尚不确定是否能够安排 $n$ 座房屋，使得所有 $n$ 位巫师的拜访和视野要求都能被满足，因此他们请求你帮忙设计这样一个方案。 如果存在一种合法的房屋摆放方式，使得对于每位第 $i$ 位巫师，都存在一座距离其房屋恰好为 $a_{i}$ 的房屋，并且第 $i$ 位巫师的房屋是其所在列唯一的房屋，则输出 YES，并输出每位巫师房屋的位置，以及每位巫师周末应拜访哪位巫师的房屋。 如果不存在合法的摆放方式，则输出 NO。

第一行包含一个整数 $n$（$2 \leq n \leq 2\cdot 10^{5}$），表示要建造的房屋数量。 第二行包含 $n$ 个整数 $a_{1}, \ldots, a_{n}$（$0 \leq a_{i} \leq n$），且 $a_{1} = 0$。

如果存在合法的摆放方式，第一行输出 YES，否则输出 NO。 如果答案为 YES，接下来输出 $n+1$ 行描述房屋的摆放方式。 接下来的 $n$ 行，每行包含两个整数，表示每位巫师房屋的坐标 $1 \leq x_{i}, y_{i} \leq n$。 最后一行包含 $n$ 个整数，第 $i$ 个数表示第 $i$ 位巫师在周末应拜访哪位巫师的房屋（即该房屋与其房屋的距离恰好为 $a_{i}$）。如果有多种选择，可以输出任意一种。 如果存在多种房屋摆放方案，可以输出任意一种。

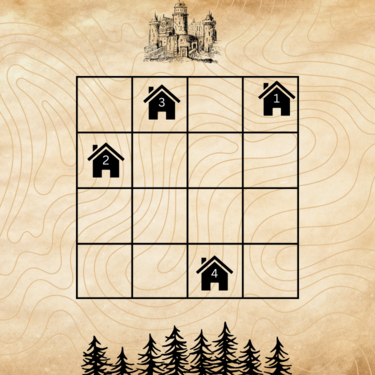
对于样例，第一位巫师的房屋位于 $(4, 4)$，第二位巫师的房屋位于 $(1, 3)$，第三位巫师的房屋位于 $(2, 4)$，第四位巫师的房屋位于 $(3, 1)$。 第一位巫师的房屋到自己的房屋距离为 $|4 - 4| + |4 - 4| = 0$。 第二位巫师的房屋到第一位巫师的房屋距离为 $|1 - 4| + |3 - 4| = 4$。 第三位巫师的房屋到第一位巫师的房屋距离为 $|2 - 4| + |4 - 4| = 2$。 第四位巫师的房屋到第三位巫师的房屋距离为 $|3 - 2| + |1 - 4| = 4$。 所有房屋都满足视野和距离要求，因此该摆放方案是正确的。  由 ChatGPT 4.1 翻译