CF1970G2 Min-Fund Prison (Medium)

现给出一张由 $n$ 个点 $m$ 条边构成的无向图，其 $m$ 条边为 $(u_i, v_i)$ ( $1\leq i\leq m$ )，表示 $u_i,v_i$ 相连。图中不存在重边，也没有自环。 你可以以 $c$ 的成本在任意两个点 $x, y$ 之间连一条边。这个操作可以进行任意次，设你操作了 $k$ 次。要求操作结束后图是连通的。 在连边操作之后，你必须删去一条割边，使得剩下的图恰由 $2$ 个连通块组成。设两个连通块的大小为 $x,y$ ，请问 $x^2+y^2+kc$ 的最小值为何？

第一行输入样例个数 $t$ ( $1\leq t\leq 300$ ) 。接下来输入 $t$ 个样例，每个样例形式如下—— 每个样例的第一行包含三个整数 $n, m, c$ ( $2\leq n\leq 300, 1\leq m\leq 300, 1\leq c\leq 10^9$ )，表示点数、边数和加边操作的成本。 接下来 $m$ 行，每一行输入两个整数 $u, v$ ( $1\leq u,v\leq n,u\neq v$ )，表示 $u,v$ 之间有一条边。 保证对于所有输入的样例，满足 $\sum n\leq 300,\sum m\leq 300$ 。

如果能够使得最后结果为两个连通块，输出 $x^2+y^2+kc$ 的最小值；否则，输出 $-1$ 。

In the first test case of the sample input, there is no way to divide the prison according to the Ministry's requirements. In the second test case, consider the corridor between cells $ 1 $ and $ 5 $ as the connection between the $ 2 $ complexes consisting of $ \{2, 3, 5, 6\} $ and $ \{1, 4\} $ cells respectively. There are no new corridors built. The total funding is $ 4^2 + 2^2 = 20 $ . You can verify this is the minimum funding required. 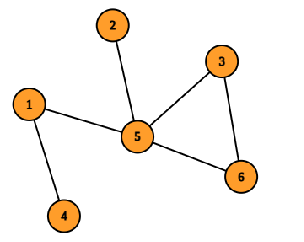 In the third test case, build a corridor between $ 2 $ and $ 4 $ . Consider the corridor between cells $ 1 $ and $ 5 $ as the connection between the $ 2 $ complexes consisting of $ \{3, 5, 6\} $ and $ \{1, 2, 4\} $ cells respectively. The total funding is $ 3^2 + 3^2 + 7 \times 1 = 25 $ . You can verify this is the minimum funding required. 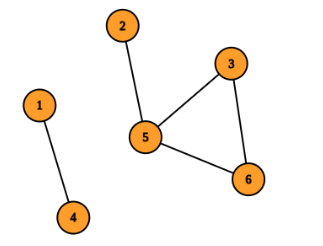 In the fourth test case, build a corridor between $ 2 $ and $ 4 $ and between $ 5 $ and $ 7 $ . Consider the corridor between cells $ 5 $ and $ 7 $ as the connection between the $ 2 $ complexes consisting of $ \{1, 2, 4, 7\} $ and $ \{3, 5, 6\} $ cells respectively. The total funding is $ 4^2 + 3^2 + 4 \times 2 = 33 $ . You can verify this is the minimum funding required. 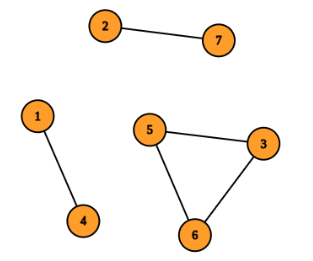 Note for all test cases that there may be multiple ways to get the same funding but there is no other division which will have a more optimal minimum funding.