CF1971D Binary Cut

给定一个二进制字符串 $ ^{\dagger} $ 。请找到您需要将其切割成的最小片段数，将生成的片段重新排列成有序的二进制字符串。  请注意： - 每个字符必须恰好位于其中一个片段中； - 这些片段必须是原始字符串的连续子字符串； - 你必须在重排中使用所有的片段。 $^{\dagger}$二进制字符串是由字符 $ \texttt{0}$ 和 $\texttt{1}$ 组成的字符串。排序后的二进制字符串是一个二进制字符串，使得所有字符 $\texttt{0}$ 位于所有字符 $\texttt{1}$ 之前。

第一行包含一个整数 $t$（$1\leq t\leq 500$）——测试用例的数量。 每个测试用例的唯一一行包含一个由 $\texttt{0}$ 和 $\texttt1$ 组成的字符串 $s$ （$1 \leq |s| \leq 500$），其中 $|s|$ 表示字符串 $s$ 的长度。

对于每个测试用例，输出将字符串重新排列为有序二进制字符串所需的最小分割数量。

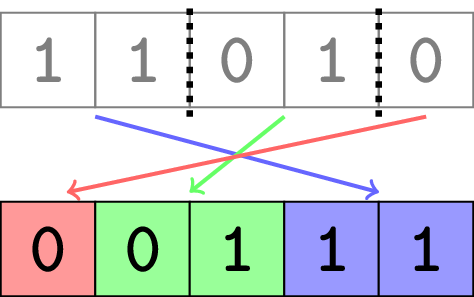
The first test case is pictured in the statement. It can be proven that you can't use fewer than $ 3 $ pieces. In the second and third test cases, the binary string is already sorted, so only $ 1 $ piece is needed. In the fourth test case, you need to make a single cut between the two characters and rearrange them to make the string $ \texttt{01} $ .