CF1971D Binary Cut

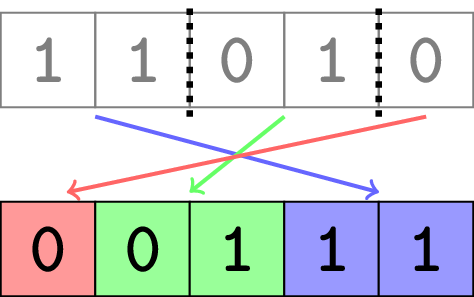You are given a binary string $ ^{\dagger} $ . Please find the minimum number of pieces you need to cut it into, so that the resulting pieces can be rearranged into a sorted binary string. Note that: - each character must lie in exactly one of the pieces; - the pieces must be contiguous substrings of the original string; - you must use all the pieces in the rearrangement. $ ^{\dagger} $ A binary string is a string consisting of characters $ \texttt{0} $ and $ \texttt{1} $ . A sorted binary string is a binary string such that all characters $ \texttt{0} $ come before all characters $ \texttt{1} $ .

The first line contains a single integer $ t $ ( $ 1 \leq t \leq 500 $ ) — the number of test cases. The only line of each test case contains a single string $ s $ ( $ 1 \leq |s| \leq 500 $ ) consisting of characters $ \texttt{0} $ and $ \texttt{1} $ , where $ |s| $ denotes the length of the string $ s $ .

For each test case, output a single integer — the minimum number of pieces needed to be able to rearrange the string into a sorted binary string.

The first test case is pictured in the statement. It can be proven that you can't use fewer than $ 3 $ pieces. In the second and third test cases, the binary string is already sorted, so only $ 1 $ piece is needed. In the fourth test case, you need to make a single cut between the two characters and rearrange them to make the string $ \texttt{01} $ .