CF1971F Circle Perimeter

Given an integer $ r $ , find the number of lattice points that have a Euclidean distance from $ (0, 0) $ greater than or equal to $ r $ but strictly less than $ r+1 $ . A lattice point is a point with integer coordinates. The Euclidean distance from $ (0, 0) $ to the point $ (x,y) $ is $ \sqrt{x^2 + y^2} $ .

The first line contains a single integer $ t $ ( $ 1 \leq t \leq 1000 $ ) — the number of test cases. The only line of each test case contains a single integer $ r $ ( $ 1 \leq r \leq 10^5 $ ). The sum of $ r $ over all test cases does not exceed $ 10^5 $ .

For each test case, output a single integer — the number of lattice points that have an Euclidean distance $ d $ from $ (0, 0) $ such that $ r \leq d < r+1 $ .

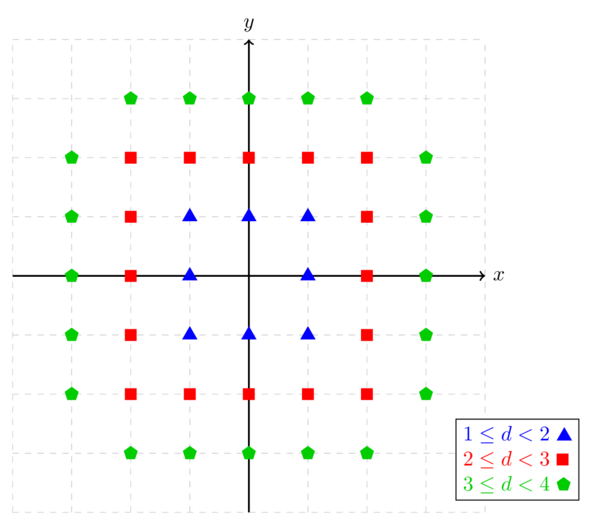
The points for the first three test cases are shown below.