CF1979E Manhattan Triangle

曼哈顿距离定义为两个点 $ (x_1, y_1) $ 和 $ (x_2, y_2) $ 之间的距离：$ |x_1 - x_2| + |y_1 - y_2| $。 我们称平面上任意三点为“曼哈顿三角形”，当且仅当这三点两两之间的曼哈顿距离都相等。 给定一组两两不同的点，以及一个偶数整数 $ d $，你的任务是从给定的点集中找出任意一个曼哈顿三角形，使得三角形的三个顶点两两之间的曼哈顿距离均为 $ d $。

每组测试数据包含多个测试用例。第一行包含一个整数 $ t $（$ 1 \le t \le 10^4 $），表示测试用例的数量。 每个测试用例的第一行包含两个整数 $ n $ 和 $ d $（$ 3 \le n \le 2 \cdot 10^5 $，$ 2 \le d \le 4 \cdot 10^5 $，$ d $ 为偶数），分别表示点的数量和要求的曼哈顿距离。 接下来的 $ n $ 行，每行包含两个整数 $ x_i $ 和 $ y_i $（$ -10^5 \le x_i, y_i \le 10^5 $），表示第 $ i $ 个点的坐标。保证所有点两两不同。 保证所有测试用例中 $ n $ 的总和不超过 $ 2 \cdot 10^5 $。

对于每个测试用例，输出三个不同的整数 $ i, j, k $（$ 1 \le i, j, k \le n $），表示构成曼哈顿三角形的三个点的编号。如果不存在满足条件的曼哈顿三角形，输出 "0 0 0"（不带引号）。 如果有多组解，输出任意一组均可。

在第一个测试用例中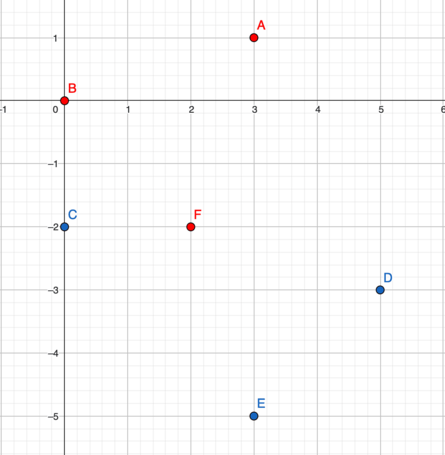：  点 $ A $、$ B $ 和 $ F $ 构成一个曼哈顿三角形，三点两两之间的曼哈顿距离均为 $ 4 $。点 $ D $、$ E $ 和 $ F $ 也可以作为答案。 在第三个测试用例中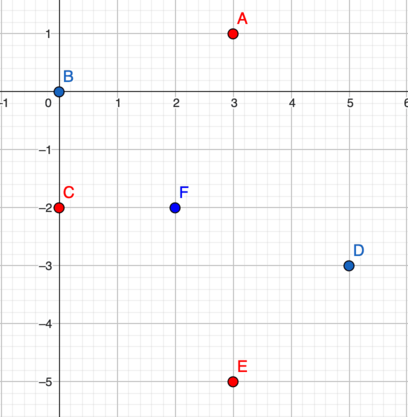：  点 $ A $、$ C $ 和 $ E $ 构成一个曼哈顿三角形，三点两两之间的曼哈顿距离均为 $ 6 $。 在第四个测试用例中，没有两点之间的曼哈顿距离为 $ 4 $，因此不存在满足条件的曼哈顿三角形。 由 ChatGPT 4.1 翻译