CF1979E Manhattan Triangle

The Manhattan distance between two points $ (x_1, y_1) $ and $ (x_2, y_2) $ is defined as: $ $$$|x_1 - x_2| + |y_1 - y_2|. $ $

We call a Manhattan triangle three points on the plane, the Manhattan distances between each pair of which are equal.

You are given a set of pairwise distinct points and an even integer $ d $ . Your task is to find any Manhattan triangle, composed of three distinct points from the given set, where the Manhattan distance between any pair of vertices is equal to $ d$$$.

Each test consists of multiple test cases. The first line contains one integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The description of the test cases follows. The first line of each test case contains two integers $ n $ and $ d $ ( $ 3 \le n \le 2 \cdot 10^5 $ , $ 2 \le d \le 4 \cdot 10^5 $ , $ d $ is even) — the number of points and the required Manhattan distance between the vertices of the triangle. The $ (i + 1) $ -th line of each test case contains two integers $ x_i $ and $ y_i $ ( $ -10^5 \le x_i, y_i \le 10^5 $ ) — the coordinates of the $ i $ -th point. It is guaranteed that all points are pairwise distinct. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

For each test case, output three distinct integers $ i $ , $ j $ , and $ k $ ( $ 1 \le i,j,k \le n $ ) — the indices of the points forming the Manhattan triangle. If there is no solution, output " $ 0\ 0\ 0 $ " (without quotes). If there are multiple solutions, output any of them.

In the first test case: 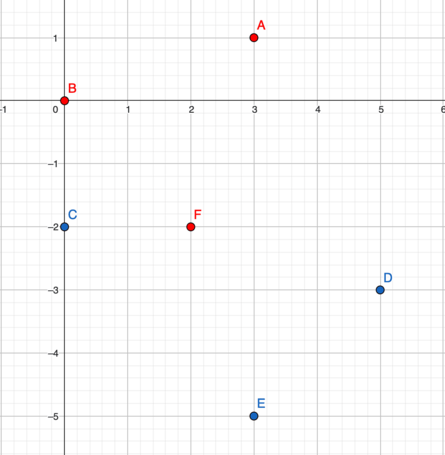 Points $ A $ , $ B $ , and $ F $ form a Manhattan triangle, the Manhattan distance between each pair of vertices is $ 4 $ . Points $ D $ , $ E $ , and $ F $ can also be the answer.In the third test case: 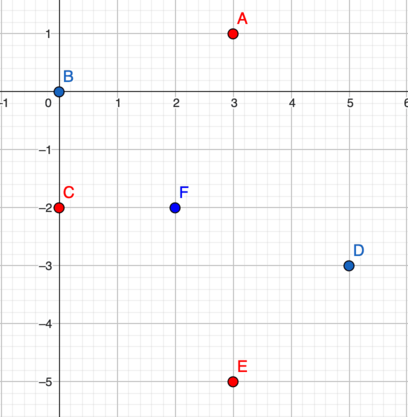 Points $ A $ , $ C $ , and $ E $ form a Manhattan triangle, the Manhattan distance between each pair of vertices is $ 6 $ .In the fourth test case, there are no two points with a Manhattan distance of $ 4 $ , and therefore there is no suitable Manhattan triangle.