CF197B Limit
Description
You are given two polynomials:
- $ P(x)=a_{0}·x^{n}+a_{1}·x^{n-1}+...+a_{n-1}·x+a_{n} $ and
- $ Q(x)=b_{0}·x^{m}+b_{1}·x^{m-1}+...+b_{m-1}·x+b_{m} $ .
Calculate limit 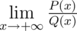.
Input Format
The first line contains two space-separated integers $ n $ and $ m $ ( $ 0
Output Format
If the limit equals $ +∞ $ , print "Infinity" (without quotes). If the limit equals $ -∞ $ , print "-Infinity" (without the quotes).
If the value of the limit equals zero, print "0/1" (without the quotes).
Otherwise, print an irreducible fraction — the value of limit 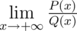, in the format "p/q" (without the quotes), where $ p $ is the — numerator, $ q $ $ (q>0) $ is the denominator of the fraction.
Explanation/Hint
Let's consider all samples:
1. 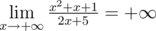
2. 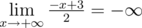
3. 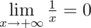
4. 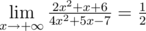
5. 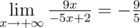
You can learn more about the definition and properties of limits if you follow the link: http://en.wikipedia.org/wiki/Limit\_of\_a\_function