CF1980F2 Field Division (hard version)

这是该问题的困难版本；它与简单版本的区别仅在于问题本身。简单版本只需要你判断某些值是否为非零，而困难版本需要你输出确切的数值。 Alice 和 Bob 正在分割一块田地。这块田地是一个 $n \times m$ 的矩形（$2 \le n, m \le 10^9$）；行从上到下编号为 $1$ 到 $n$，列从左到右编号为 $1$ 到 $m$。第 $r$ 行第 $c$ 列的格子记作 $(r, c)$。 Bob 有 $k$ 个喷泉（$2 \le k \le 2 \cdot 10^5$），所有喷泉都位于不同的格子中。Alice 负责分割田地，但她必须满足以下条件： - 为了分割田地，Alice 会从左侧或上侧任意一个没有喷泉的格子出发，每次只能向下或向右移动到相邻的格子。她的路径会在右侧或下侧的某个格子结束。 - Alice 的路径会把田地分成两部分——一部分归 Alice 所有（包括她路径上的所有格子），另一部分归 Bob 所有。 - Alice 拥有包含格子 $(n, 1)$ 的那一部分。 - Bob 拥有包含格子 $(1, m)$ 的那一部分。 Alice 希望分割田地，使她获得的格子数尽可能多。 Bob 希望保留所有喷泉，但他可以把其中一个喷泉让给 Alice。首先，输出整数 $\alpha$——在 Bob 不让出任何喷泉（即所有喷泉都归 Bob 所有）的情况下，Alice 能获得的最大格子数。 然后输出 $k$ 个非负整数 $a_1, a_2, \dots, a_k$，其中 $a_i$ 表示如果 Bob 把第 $i$ 个喷泉让给 Alice 后，Alice 能获得的最大格子数为 $\alpha + a_i$。

第一行包含一个整数 $t$（$1 \le t \le 10^4$）——表示测试用例的数量。 每个测试用例的第一行包含三个整数 $n$、$m$ 和 $k$（$2 \le n, m \le 10^9$，$2 \le k \le 2 \cdot 10^5$）——田地的大小和喷泉的数量。 接下来 $k$ 行，每行包含两个整数 $r_i$ 和 $c_i$（$1 \le r_i \le n$，$1 \le c_i \le m$）——第 $i$ 个喷泉所在格子的坐标。保证所有格子互不相同，且没有喷泉位于 $(n, 1)$。 保证所有测试用例中 $k$ 的总和不超过 $2 \cdot 10^5$。

对于每个测试用例，首先输出一个整数 $\alpha$，表示在 Bob 不让出任何喷泉的情况下，Alice 能获得的最大格子数。然后输出 $k$ 个非负整数 $a_1, a_2, \dots, a_k$，其中 $a_i$ 表示如果 Bob 把第 $i$ 个喷泉让给 Alice 后，Alice 能获得的最大格子数为 $\alpha + a_i$。

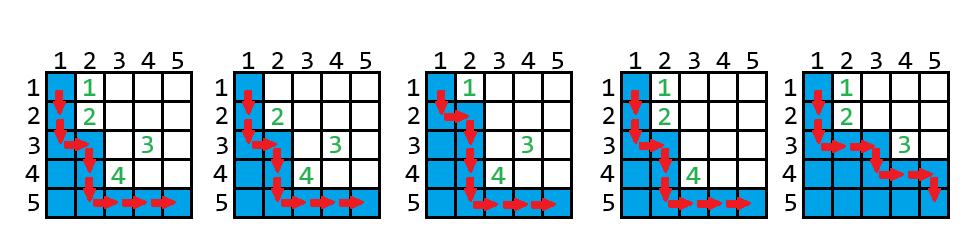
以下是第二个样例的图片说明：  喷泉的编号用绿色标注。属于 Alice 的格子用蓝色标注。注意，如果 Bob 把喷泉 $1$ 或喷泉 $3$ 让给 Alice，那么这些喷泉不能出现在 Alice 的区域中。 由 ChatGPT 4.1 翻译