CF1981E Turtle and Intersected Segments

Turtle 给你 $n$ 条线段和一个序列 $a_1,a_2,\cdots,a_n$，第 $i$ 条线段是 $[l_i,r_i]$。 Turtle 将按如下方式建图：对于任意的 $i,j$，若 $i,j$ 相交，则 $i,j$ 之间连一条边权为 $|a_i-a_j|$ 的边。相交的定义为 $\max(l_1,l_2)\le\min(r_1,r_2)$。 Turtle 想知道最小生成树的边权和是多少。 保证所有子数据 $n$ 的和不超过 $5\cdot10^5$。

一组输入数据有 $t(1\le t\le10^5)$ 组子数据。第一行输入 $t$，每组子数据格式如下： 第一行一个正整数 $n(2\le n\le 5\times 10^5)$。 接下来每行三个整数 $l_i,r_i,a_i(1\le l_i,r_i\le 10^9,1\le a_i\le 10^9)$。

对于每组子数据输出一行一个整数，表示最小生成树的边权和，若没有生成树输出 $-1$。

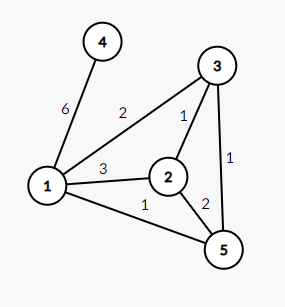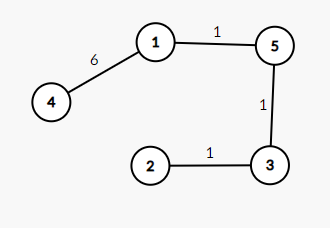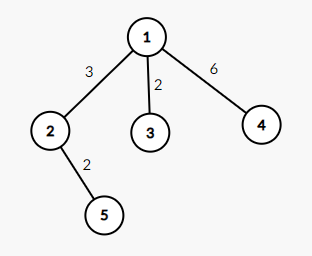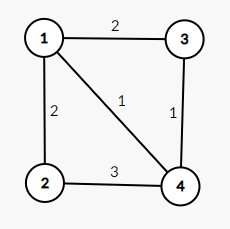In the first test case, the graph $ G $ is as follows: One of the minimum spanning trees of $ G $ is as follows: The sum of the weights of the edges of the minimum spanning tree is $ 9 $ . In the second test case, the graph $ G $ is as follows:  $ G $ is already a tree, and the sum of the weights of the tree is $ 13 $ . 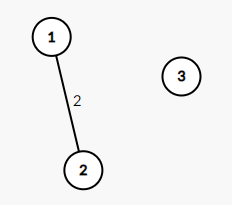In the third test case, the graph $ G $ is as follows: In the fourth test case, the graph $ G $ is as follows: It's easy to see that $ G $ is not connected, so $ G $ has no spanning tree.