CF1981E Turtle and Intersected Segments

Turtle just received $ n $ segments and a sequence $ a_1, a_2, \ldots, a_n $ . The $ i $ -th segment is $ [l_i, r_i] $ . Turtle will create an undirected graph $ G $ . If segment $ i $ and segment $ j $ intersect, then Turtle will add an undirected edge between $ i $ and $ j $ with a weight of $ |a_i - a_j| $ , for every $ i \ne j $ . Turtle wants you to calculate the sum of the weights of the edges of the minimum spanning tree of the graph $ G $ , or report that the graph $ G $ has no spanning tree. We say two segments $ [l_1, r_1] $ and $ [l_2, r_2] $ intersect if and only if $ \max(l_1, l_2) \le \min(r_1, r_2) $ .

Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^5 $ ). The description of the test cases follows. The first line of each test case contains a single integer $ n $ ( $ 2 \le n \le 5 \cdot 10^5 $ ) — the number of segments. The $ i $ -th of the following $ n $ lines contains three integers $ l_i, r_i, a_i $ ( $ 1 \le l_i \le r_i \le 10^9, 1 \le a_i \le 10^9 $ ) — the $ i $ -th segment and the $ i $ -th element of the sequence. It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 5 \cdot 10^5 $ .

For each test case, output a single integer — the sum of the weights of the edges of the minimum spanning tree of the graph $ G $ . If the graph $ G $ has no spanning tree, output $ -1 $ .

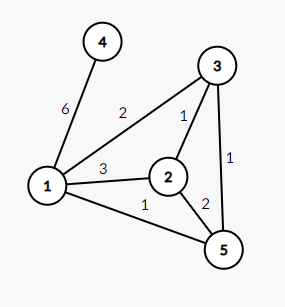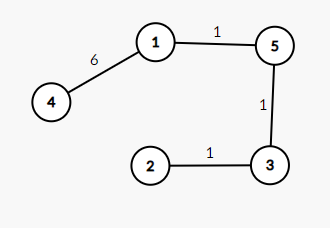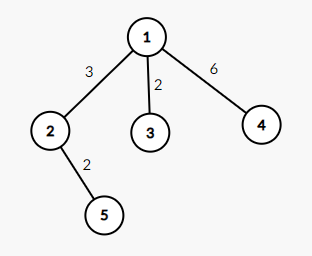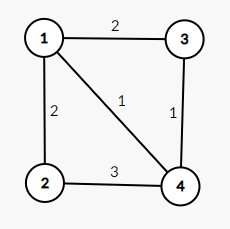In the first test case, the graph $ G $ is as follows: One of the minimum spanning trees of $ G $ is as follows: The sum of the weights of the edges of the minimum spanning tree is $ 9 $ . In the second test case, the graph $ G $ is as follows:  $ G $ is already a tree, and the sum of the weights of the tree is $ 13 $ . 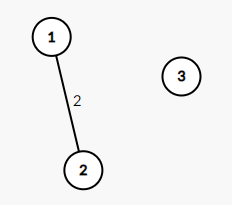In the third test case, the graph $ G $ is as follows: In the fourth test case, the graph $ G $ is as follows: It's easy to see that $ G $ is not connected, so $ G $ has no spanning tree.